边缘检测原理
概述
- 以灰度局部剧烈变化为基础,检测图像中的点、线边缘。
- 用一阶微分和二阶微分为工具来达到检测目的
原理
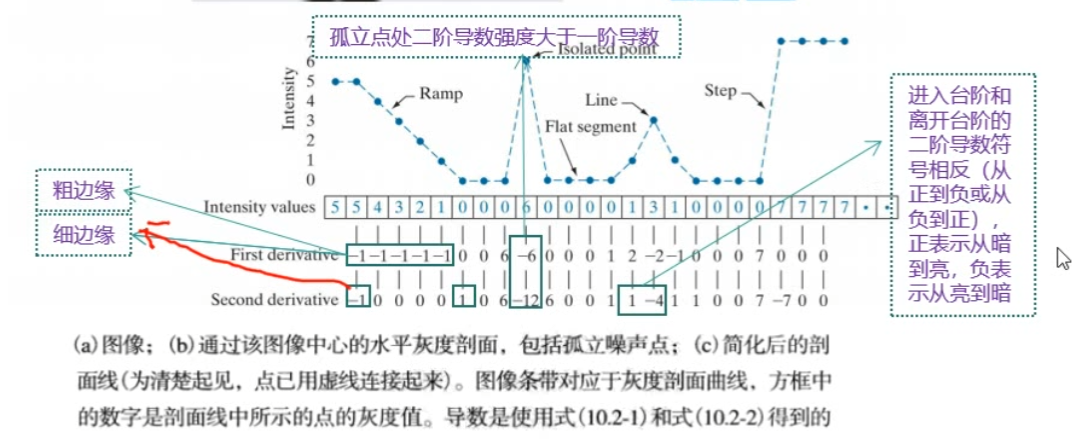
- 一阶导数产生较粗的边缘
- 二阶导数对精细细节如细线、孤立点和噪声有较强响应
- 二阶导数在灰度斜坡和灰度台阶处会产生双边缘效应
- 二阶导数的符号可以确定是从亮到暗还是从暗到亮
检测孤立点
原理
用二阶导数检测孤立点,用拉普拉斯算子

过程
- 对输入图像用拉普拉斯核进行卷积
- 对卷积结果按如下公式操作,得到阈值处理结果
检测线
- 由于二阶导数的响应更加强烈,因此拉普拉斯算子可以用于检测线
- 检测线时,要根据待检测的线宽设计拉普拉斯核的尺
- 拉普拉斯核是各向同性的,没办法检测特定方向的线
- 优先
- 各向同性,线性和位移不变的
- 对细线和孤立点的检测效果较好
- 缺点
- 对噪声的敏感,对噪声有双倍加强作用
- 不能检测出边的方向
- 常产生双像素的边缘
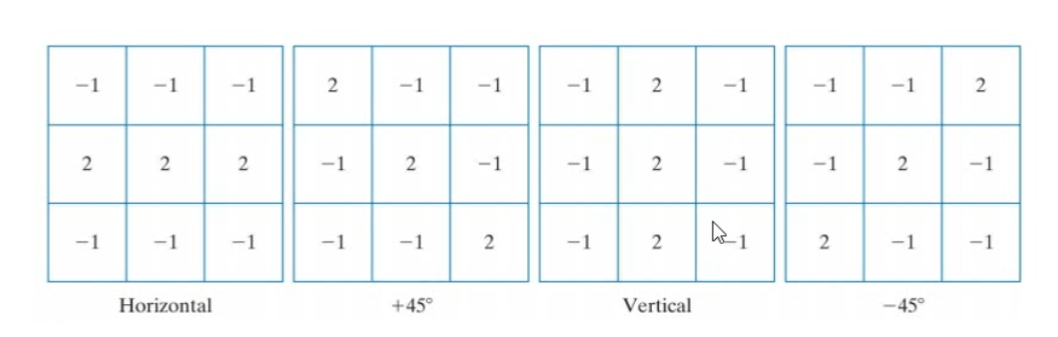
- 用如下的二阶偏导来计算不同方向的线
边缘检测
边缘模型
基于灰度突变来定位边缘位置
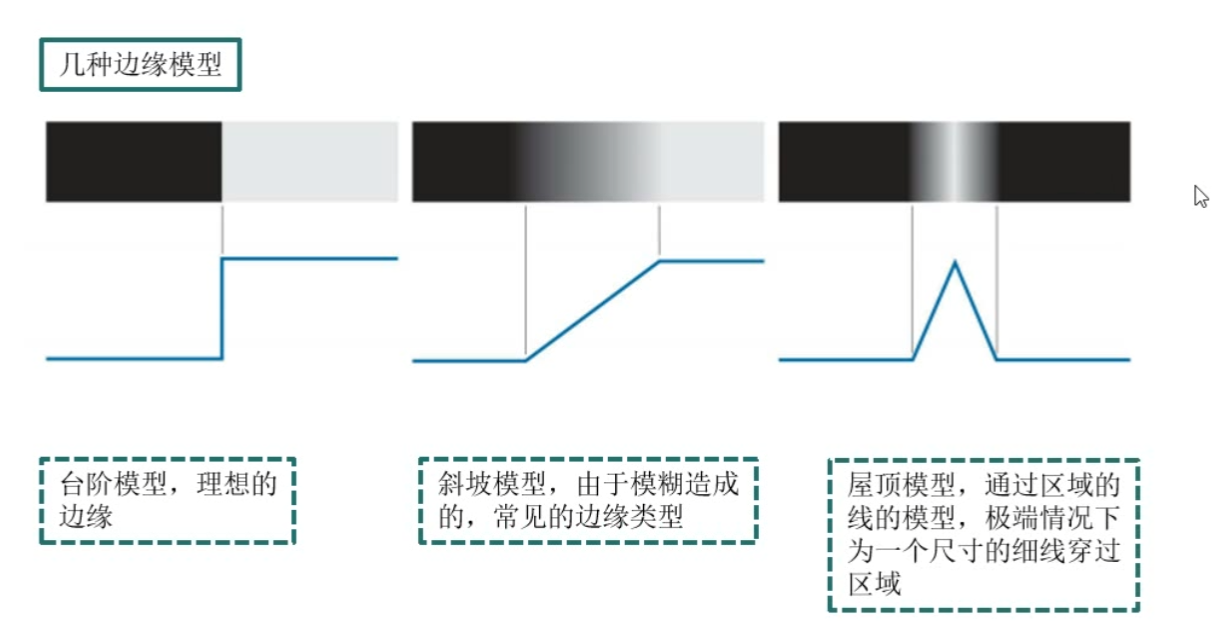
找边缘时降噪很重要
边缘检测步骤
- 降噪,通过高斯滤波器、均值滤波器、中值滤波器等算子对图像进行平滑处理
- 边缘点的检测
- 边缘定位
边缘检测的方法
- 基于梯度算子,如prewitter,sobel
- loG算子检测(高斯拉普拉斯)又称为Marr-Hildreth检测器
- Canny算子检测
基于梯度算子检测
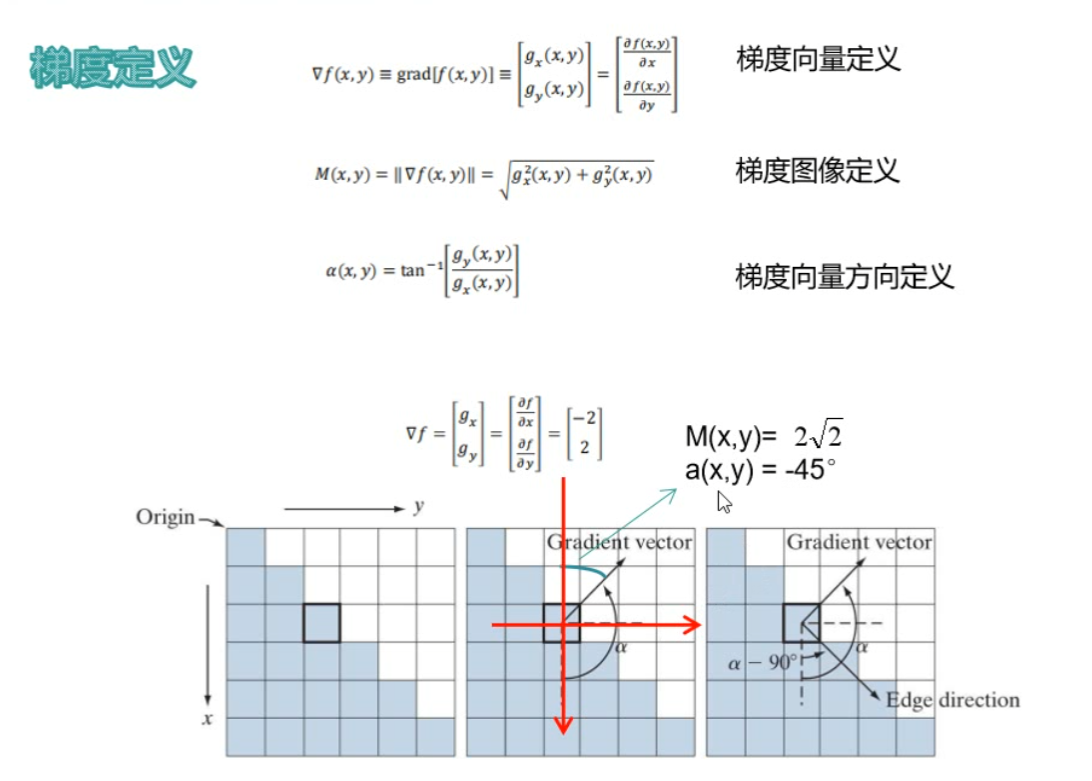
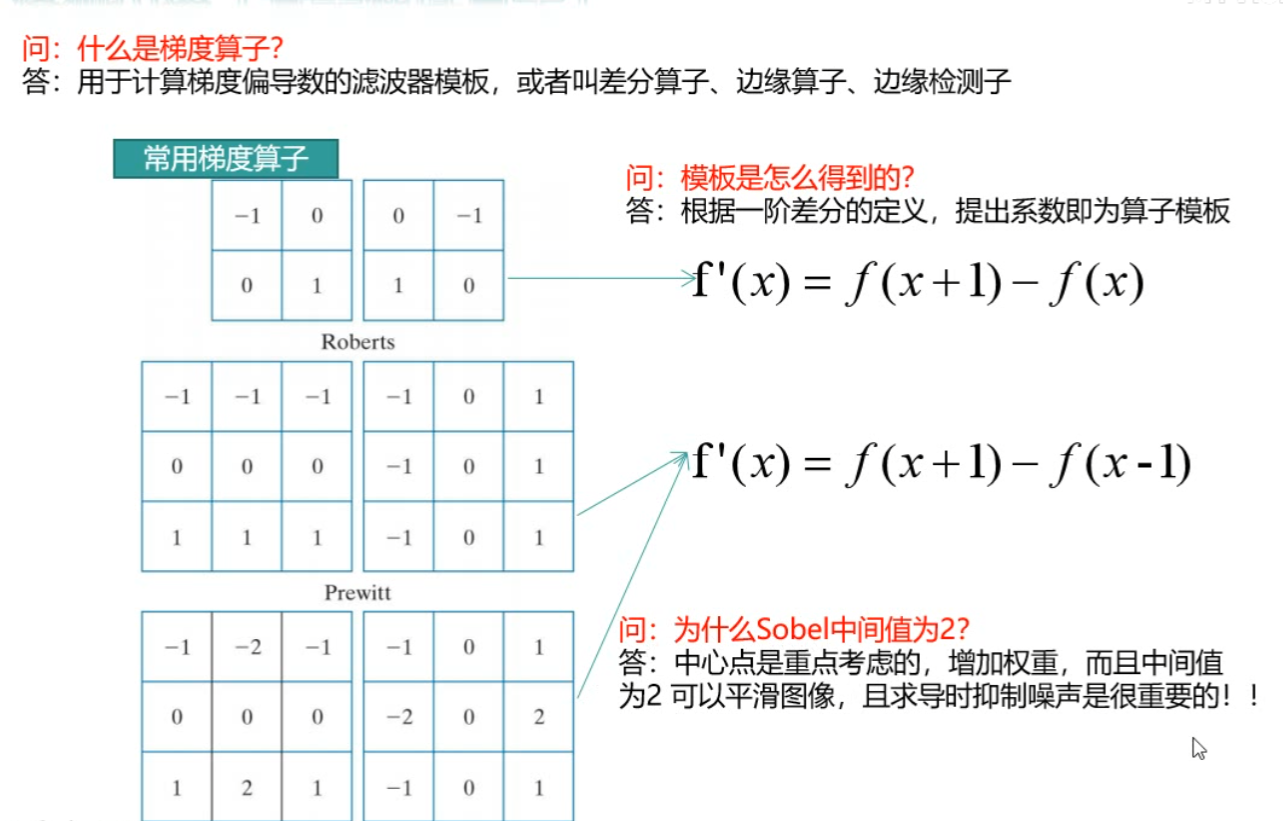
不足:未对图像噪声和边缘本身特性采取预防措施
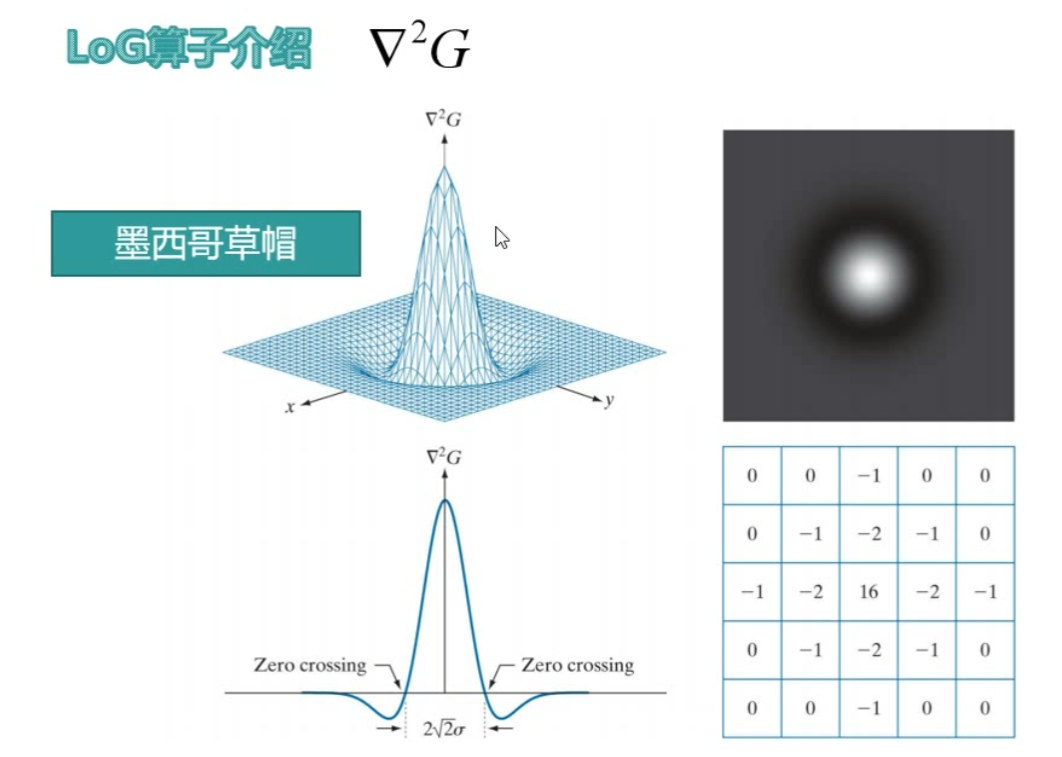
loG算子检测
- 灰度变化与图像尺寸无关,因此可以使用不同尺寸的算子(而不仅仅是小算子如3, 5,7),而取决于数值范围
- 灰度的突然变化会在一阶导数中引起波峰或波谷,在二阶导数中等效地引起零交叉
- 因此,算子应具备以下特征
- 能计算图像中任一个位置的一阶和二阶微分的算子
- 它的尺寸可以被调整,以便在任何期望的尺寸上起作用,大的算子可以检测模糊边缘,小的算子可以检测精细细节。
- 因此LoG算子应运而生

Canny算子检测
特点
- 低错误率,所有的边缘点都被找到
- 边缘点被很好的定位
- 单一的边缘响应(正式边缘周围只返回一个点)
过程
- 用高斯滤波器平滑输入图像
- 计算梯度复读图像和角度图像
- 对复读图像应用非最大抑制
- 用双阈值处理和连接分析来检测并连接边缘
边缘连接
概述
由于前述方法检测完得到的可能是不连续的边界,这里的目的是将不连续的边界连接为闭合的边界,因此边缘检测之后紧跟连接算法
边缘连接的方法有哪些:
- 局部处理
- 区域处理
- 全局处理
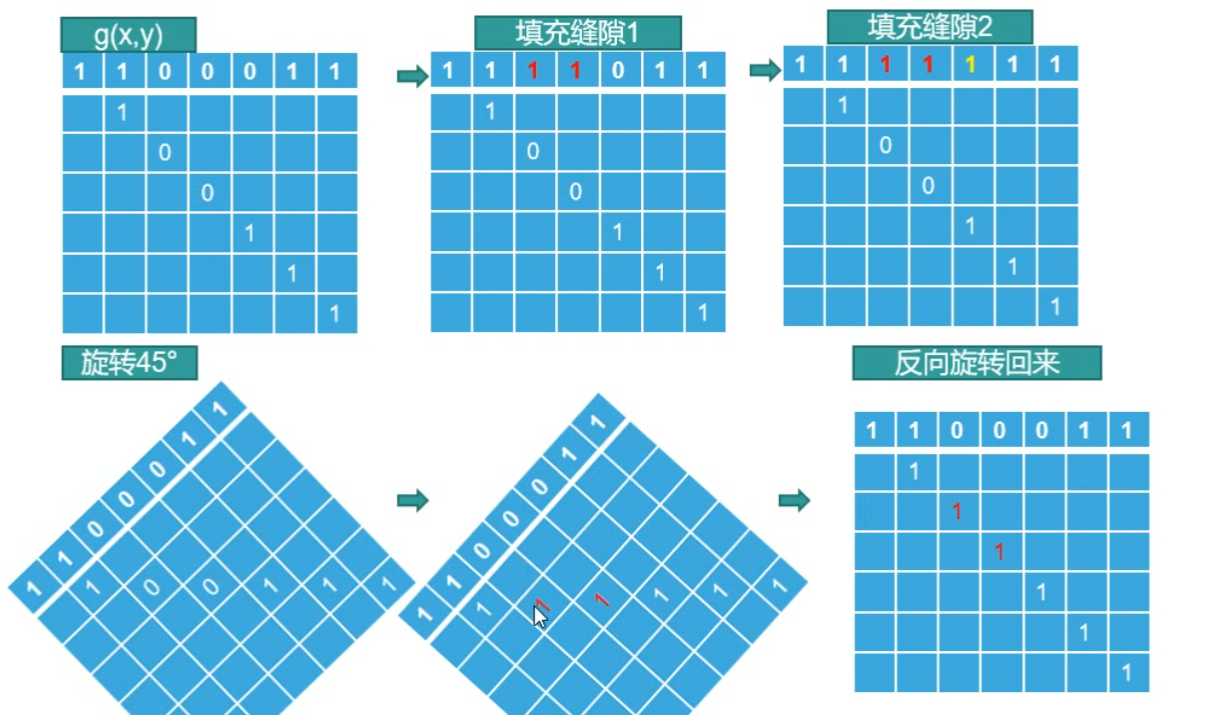
局部处理

举个例子,假设k=2
全局处理
- 因为有时候需要处理的图像没有任何区域边界信息,原理是基于像素集是否位于指定形状的曲线上的方法,一旦检测到,这些曲线就会变成感兴趣的点
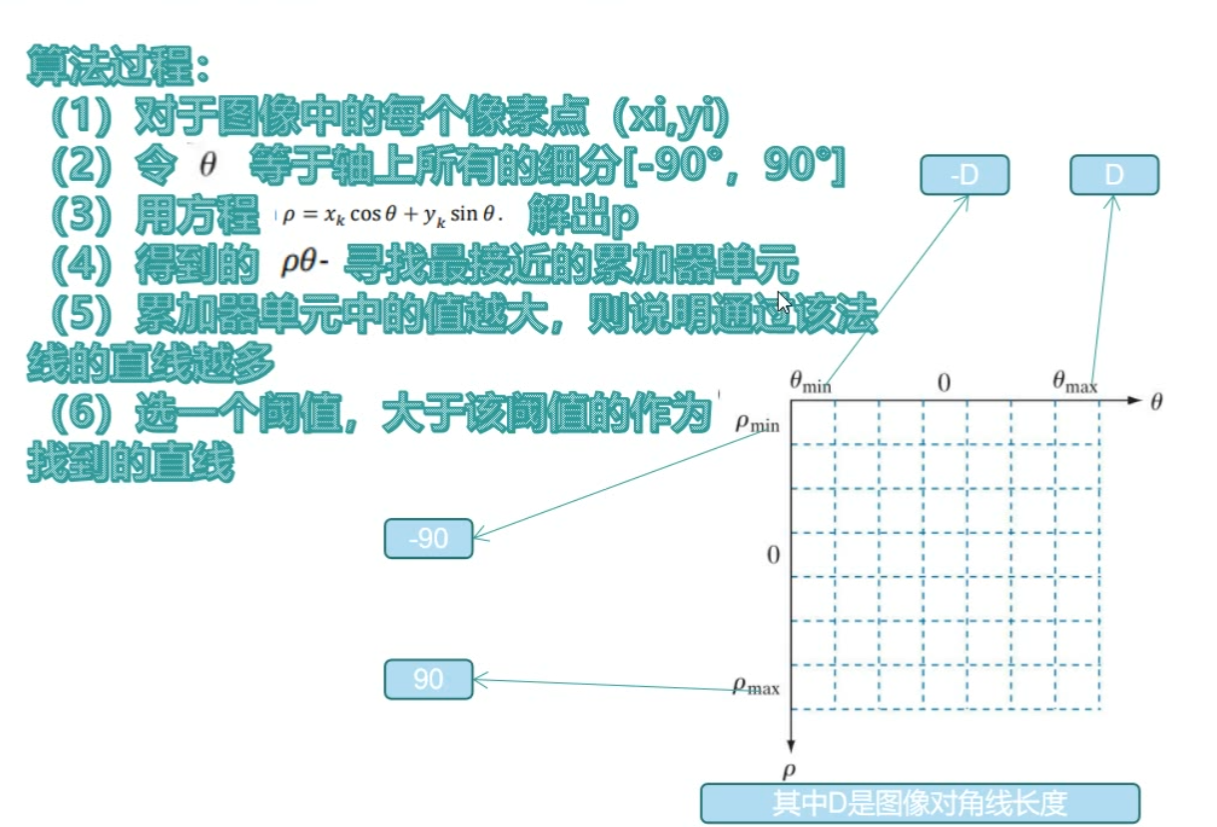
- 全局处理常用Hough变换
- Hough变换可以用于将边缘像素连接起来得到边界曲线,优点在于收噪声和曲线尖端的影响较小
- 在已知曲线形状的条件下,Hough变换实际上是利用分散的边缘点进行曲线逼近,它也可看成是一种聚类分析技术

参考资料
https://www.bilibili.com/video/BV19F411T7fD(本系列文章就是根据链接里的教程进行整理)








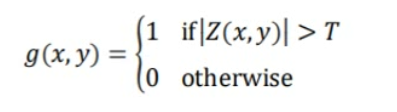


Comments | 0 条评论