目录
光栅化
如何定义视椎体宽高比和垂直可视角度?
fov:垂直可视角度
t:在y轴的高度
n:近平面上的z轴上的点
tan(fov/2)= t/|n|
r:中心点到右边的距离
宽高比(aspect) = 2r/2t = r/t
如何将投射完成的标准立方体显示到屏幕上?
什么是屏幕?
- 二维数组
- 每个元素是一个像素
- 一种经典的光栅成像设备
光栅化:在屏幕上绘画
像素:
- 在屏幕上最小单位的小方块
- 由红绿蓝三原色混合而成
屏幕空间
- 像素都是以(x,y)的形式表示,其中x、y都是整数
- 像素的范围从(0,0)到(宽度-1,长度-1)
- 像素的中心在(x+0.5,y+0.5)
- 屏幕覆盖范围为(0, 0) 到 (宽, 高)
视口变换
- Z轴被忽略
- 将原本【-1,1】²的正方体变换为【0,宽】x【0,高】(视口变换)
- 视口变换矩阵
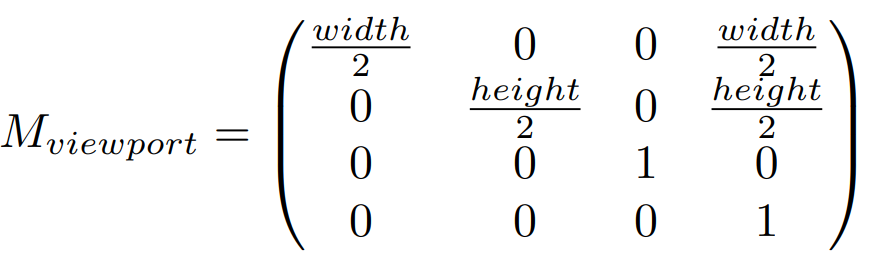
光栅显示设备
- 阴极射线管
- 隔行扫描方法
- CRT显示器
- 示波器
- 帧缓冲器
- 平板显示设备
- LCD(液晶显示器)
- OLED
- LED(发光二极管)
- 电子墨水屏
三角形-基本形状单元
- 最基础的多边形
- 任何多边形都可以
- 独特的性质
- 除非折成两个三角形,否则永远是一个面
- 三角形的内外很明确
- 可以利用重心插值进行三角形顶点插值
采样
在某个点对函数求值就是采样,我们通过采样将函数离散化。
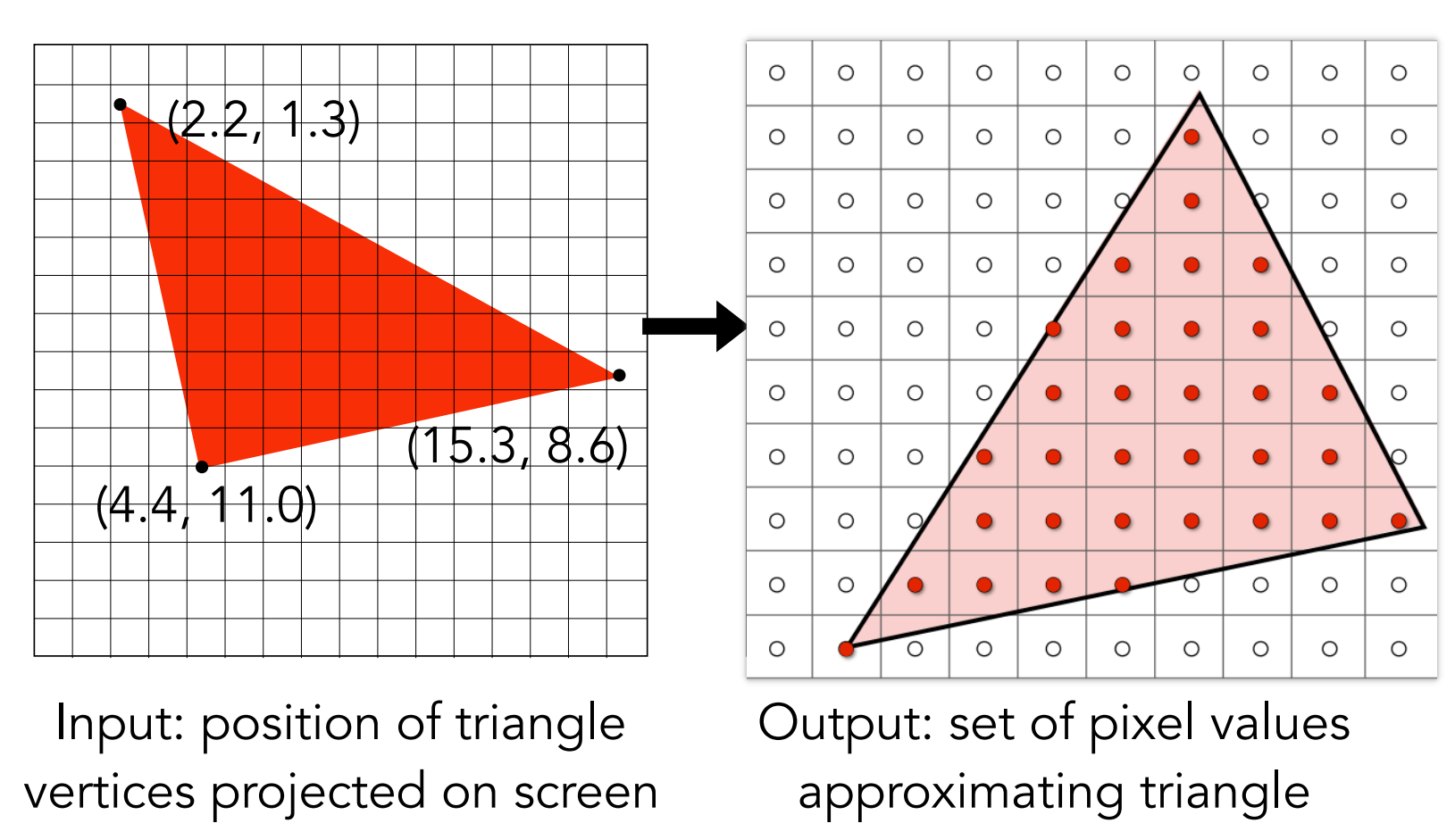
Inside函数
inside(tri,x,y)
1:point(x,y)在三角形内
0:其余情况
遍历所有点,判断所有点是否在像素内
for(int x = 0; x < xmax; ++x)
{
for(int y = 0; y < ymax; ++y)
{
image[x][y] = inside(tri, x + 0.5, y + 0.5);
}
}
通过叉乘计算出(见叉乘在图形学的应用)点是否在三角形内
如果碰巧点在三角形的边界,本课程中不做处理,也可以特殊处理
包围盒优化
利用包围盒(Bounding Box)对一定不会包含三角形的像素进行优化
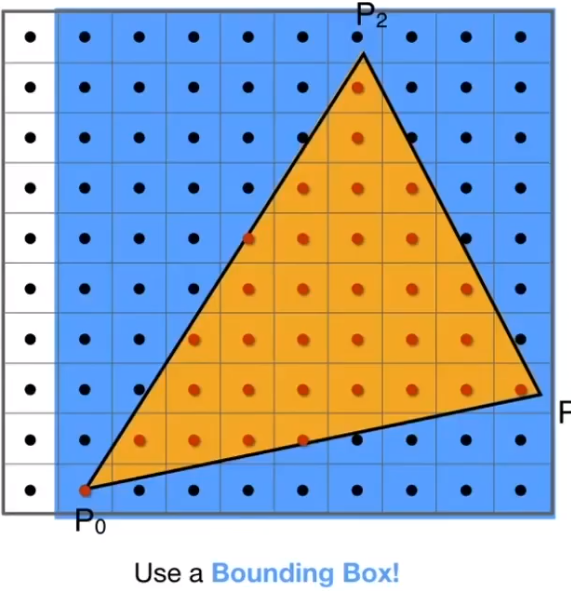
对于窄长的三角形并不友好
采样的瑕疵
- 锯齿

通过inside函数渲染出来的三角形有明显锯齿
抗锯齿是图形学中重要的难题
通过对原本三角形做模糊处理再进行采样可以抗锯齿(反走样)
不能先采样再做模糊
之所以会出现锯齿(走样)是因为出现了频谱混叠(后面有讲)
- 摩尔纹

- 车轮效应
信号时间变化太快以至于采样跟不上变化的速度
时域与频域
频域是描述信号在频率方面特性时用到的一种坐标系
时域是描述数学函数或物理信号对时间的关系的一种坐标系。
傅里叶级数展开
傅里叶变换会将时域转化为频域
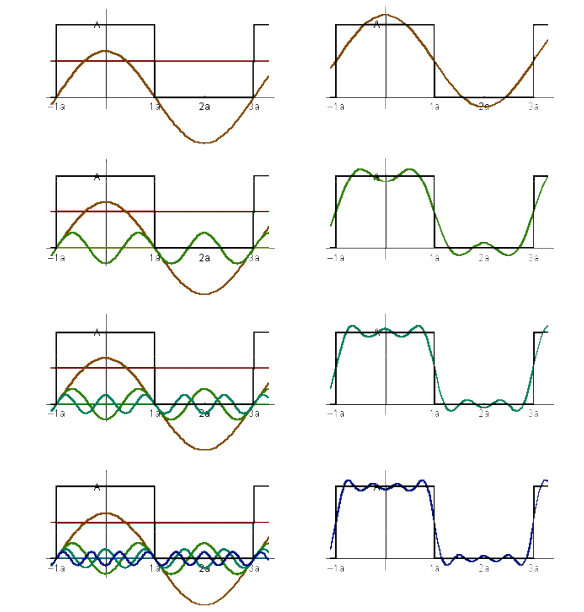
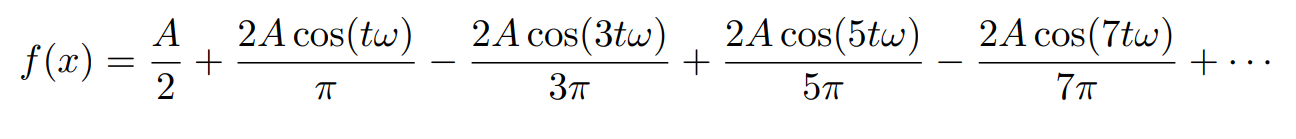
将函数表示为正弦余弦的加权和
随着展开式越来越多,越来越接近我们想要表达的函数
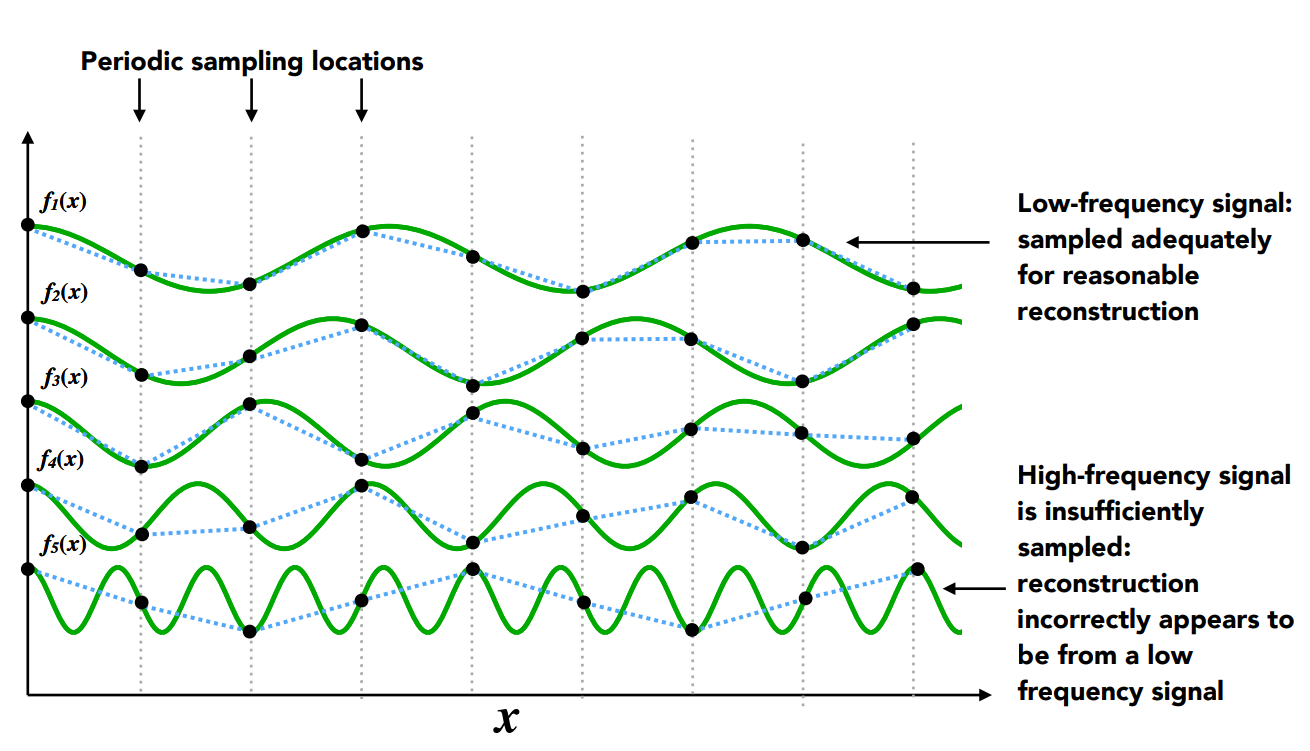
如果采样的频率不够,还原过来的函数就会越来越不精准
频域和时域可以通过傅里叶变换和逆变换互相转换
傅里叶频域图

滤波
删除特定的频率被称之为滤波
高通滤波:只显示高频信息(只显示边界-锐化),将低频信息盖住
低通滤波:只显示低频滤波(画面变模糊),将高频信息盖住
卷积
滤波=卷积(=平均)
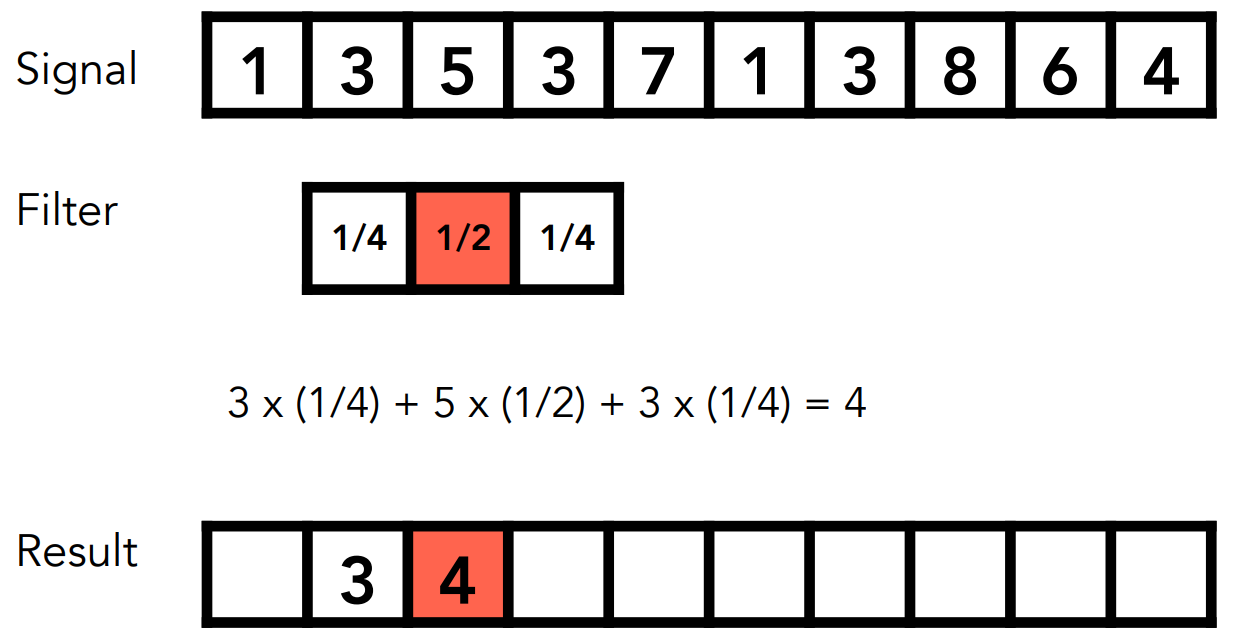
简化的定义:结果为相邻数的平均值
定理:时域的卷积等于频域的乘积
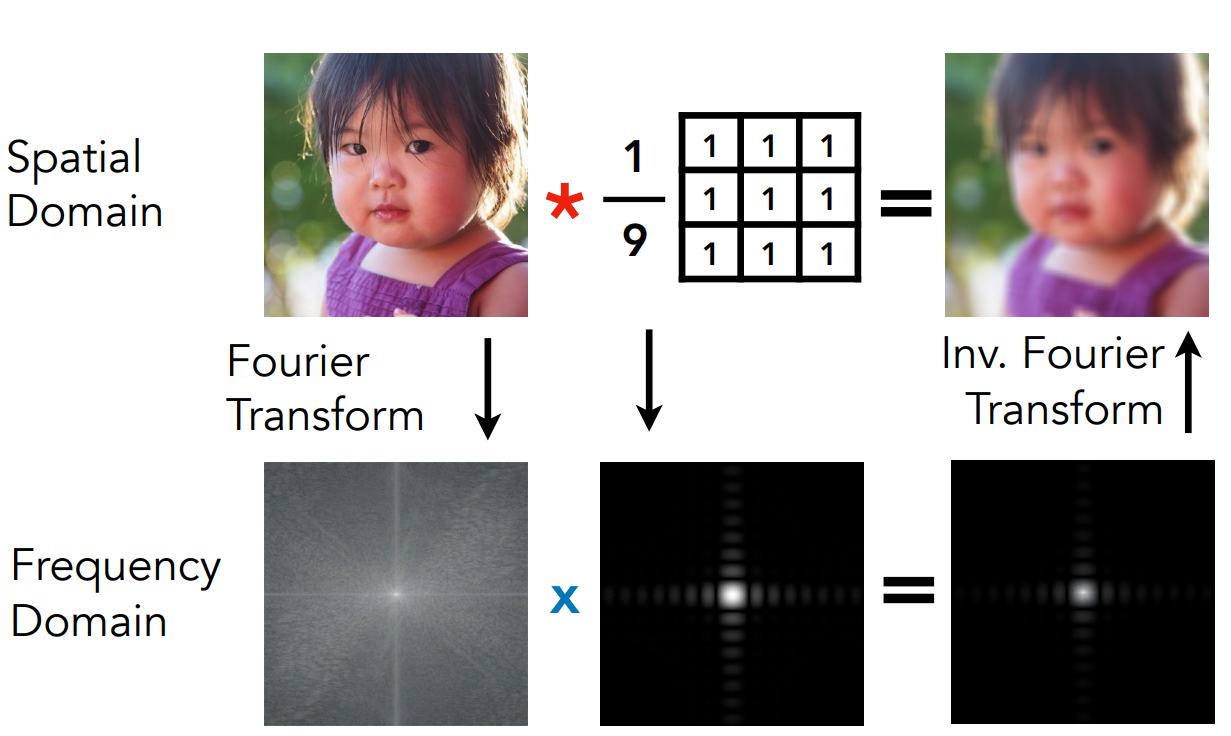
频谱混叠
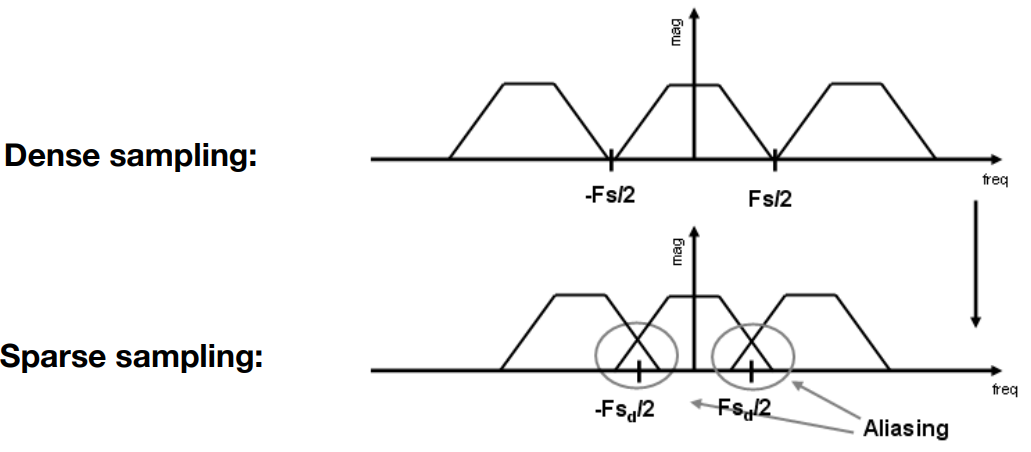
由于采样稀疏,因此出现频谱混叠从而出现锯齿(走样)如果屏幕中像素非常多,密集的采样就不容易出现走样。
因此使用分辨率高的显示器,频谱的搬移间隔大,不容易出现频谱混叠。
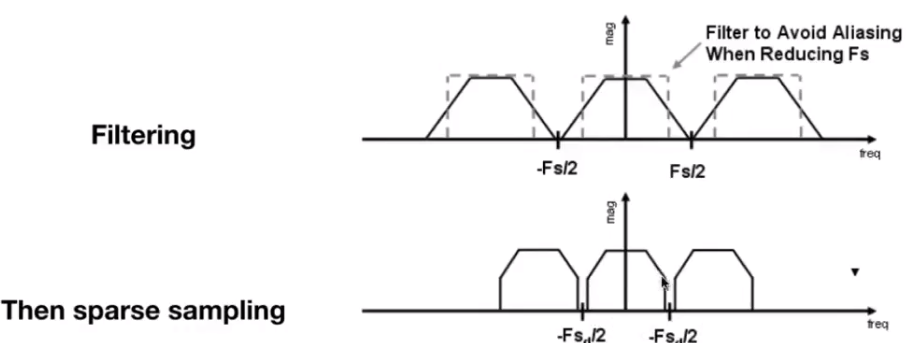
同时,将信息进行低通采样再进行采样即可反走样。
反走样(抗锯齿)
解决方法:
- 通过将每个像素进行模糊卷积f(x,y)
- 卷积=滤波=平均
- 然后再对灭个像素的中心取样
在光栅化一个三角形时,像素颜色的平均值f(x,y)= 三角形的覆盖像素的面积
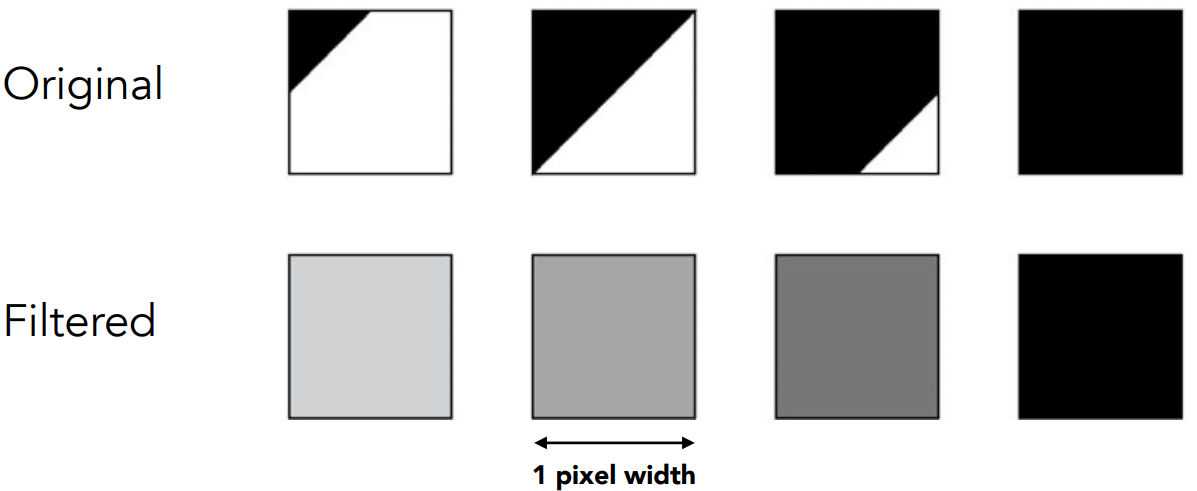
超采样抗锯齿(MSAA)
MSAA: Antialiasing By Supersampling
这是一种对反走样的近似
将每个像素的内部多增加采样点再进行模糊卷积
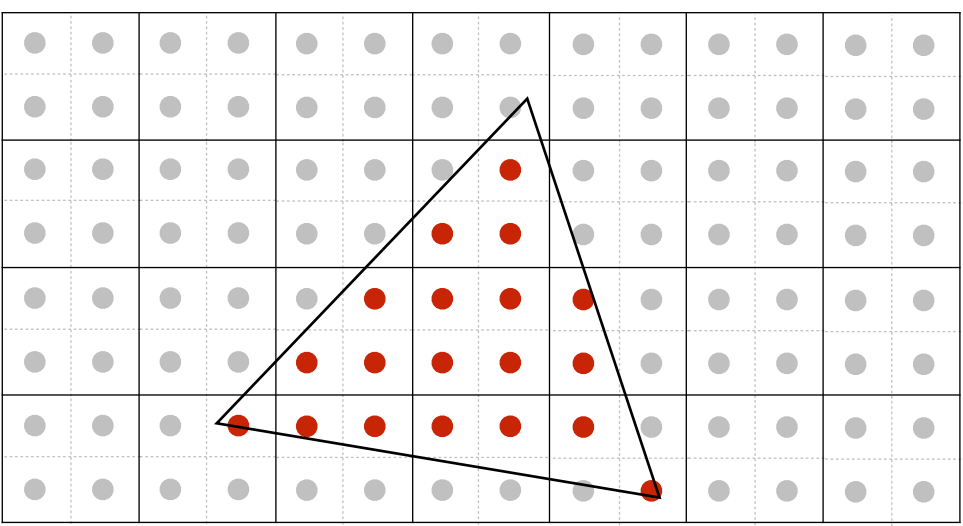
MSAA X4
缺点:增加了很多的计算量
其他的抗锯齿方法
- FXAA (Fast Approximate AA)
- 快速近似抗锯齿
- 图像的快速处理
- TAA (Temporal AA)
- 对上一帧进行处理
超分辨率
从低分辨率处理成高分辨率
与反走样类似,也是解决了样本不足的问题
目前可使用DLSS(深度学习的方法)进行超分辨率处理
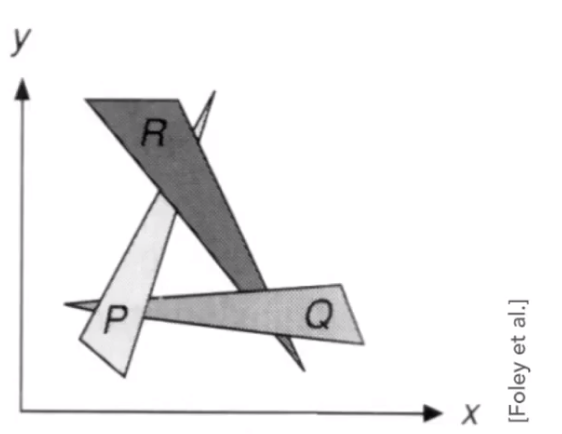
画家算法
灵感来源于画优化
先画(渲染)距离远的,再画(渲染)距离近的。
问题:难以确定谁在前谁在后
深度缓冲(Z-Buffer)
- 深度图-储存每个像素对应的最浅的深度
- 结果图-储存最终的结果
特别定义:Z越小(越黑)越近,越大越远(与通常的右手系不同,仅仅为了便于理解)

算法:
//默认深度为无限远
for(each triangle T)
{
for(each sample(x,y,z) in T)//遍历任意一个三角形中的任意一个像素
{
if(z<zbuffer[x,y])//如果此时的深度小于之前记录好的深度
{
framebuffer[x,y] = rgb;//三角形着色
zbuffer[x,y] = z;//更新小的深度
}
else
{
//...
}
}
}











 加油
加油

