线性表的定义和基本操作

定义：

  • 线性表(Linear List)是具有相同数据类型的n（n≥0）个数据元素的有限序列，其中n为表长，当n = 0时线性表是一个空表
  • 若用L命名线性表，则其一般表示为L = (a1, a2, … , ai, ai+1, … , an)
  • a1是表头元素
  • an是表尾元素
  • 除第一个元素外，每个元素有且仅有一个直接前驱
  • 除最后一个元素外，每个元素有且仅有一个直接后继

基本操作：

  • InitList(&L)：初始化表。构造一个空的线性表L，分配内存空间。
  • DestroyList(&L)：销毁操作。销毁线性表，并释放线性表L所占用的内存空间。
  • ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。
  • ListDelete(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。
  • LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。
  • GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。
  • Length(L)：求表长。返回线性表L的长度，即L中数据元素的个数。
  • PrintList(L)：输出操作。按前后顺序输出线性表L的所有元素值。
  • Empty(L)：判空操作。若L为空表，则返回true，否则返回false。
  • 什么时候要传入参数的引用“&”： 对参数的修改结果需要“带回来”，是引用类型而不是值类型

顺序表的定义

定义：

用顺序存储的方式实现线性表顺序存储，把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

如何知道一个数据元素大小：

C语言sizeof(ElemType)

顺序表的实现-静态分配：

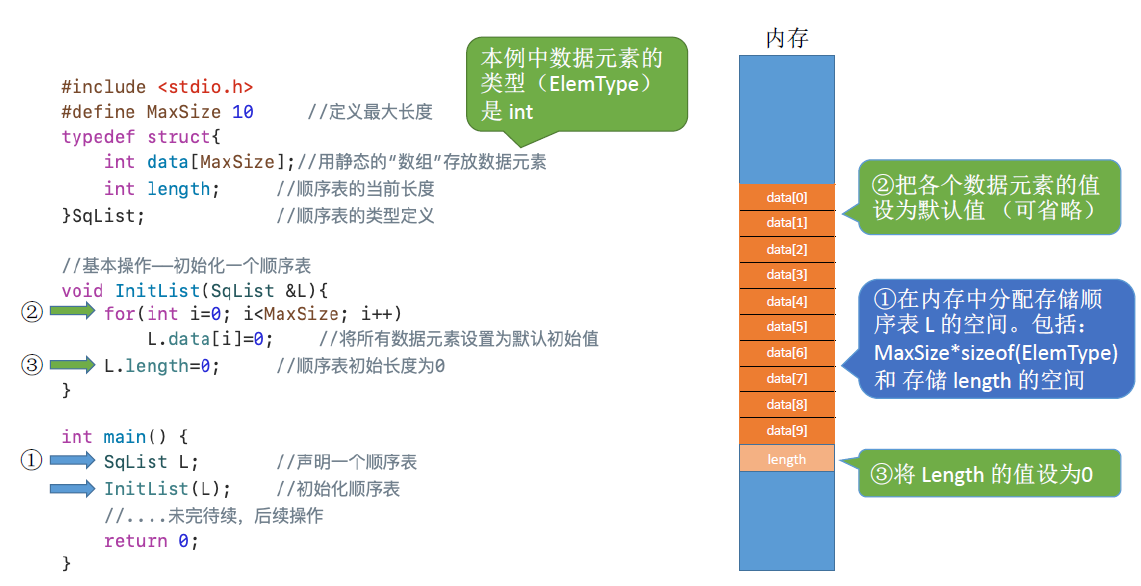
image-20220624152227262

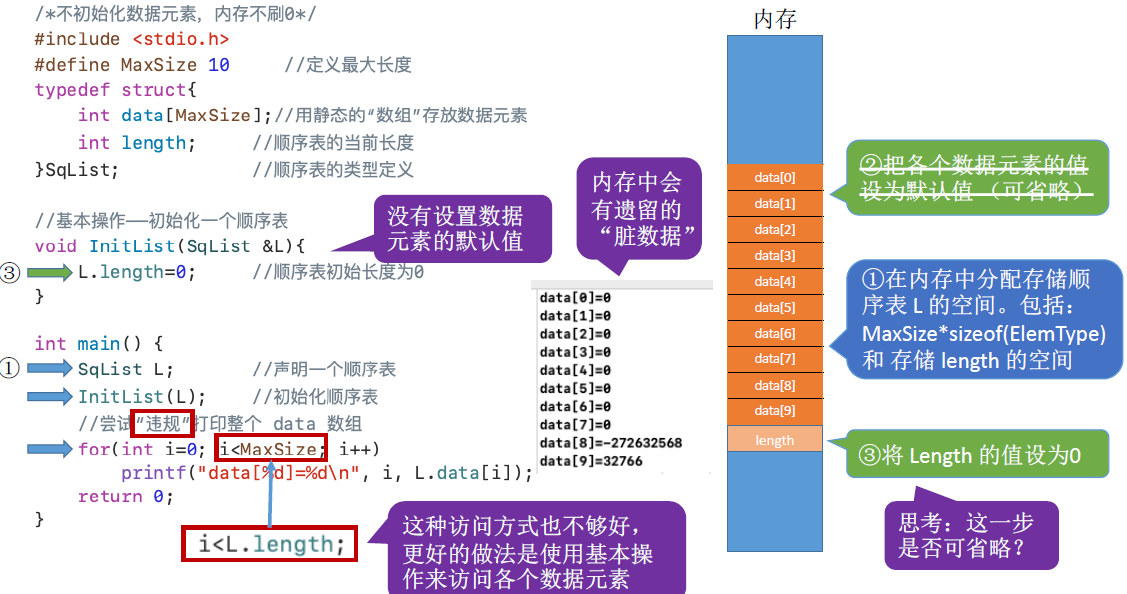
image-20220624152445049

如果“数组”存满了怎么办：

可以放弃治疗，顺序表的表长刚开始确定后就无法更改（存储空间是静态的），同时如果提前初始化太多的空间而不用，又会造成资源的浪费，因此动态分配应运而生。

动态申请和释放内存空间：

  • C：malloc、free函数
    • L.data = (ElemType *) malloc (sizeof(ElemType) * InitSize);
    • malloc函数返回一个指针， 空间需要强制转型为你定义的数据元素类型指针
    • malloc函数的参数，指明要分配多大的连续内存空间
  • C++： new、delete关键字

顺序表的实现-动态分配：

image-20220624170130119

顺序表的实现：

  • 随机访问，即可以在O(1)时间内找到第i个元素。
  • 存储密度高，每个结点只存储数据元素
  • 拓展容量不方便（即便采用动态分配的方式实现，拓展长度的时间复杂度也比较高）
  • 插入、删除操作不方便，需要移动大量元素

顺序表的插入、删除

顺序表的基本操作-插入：

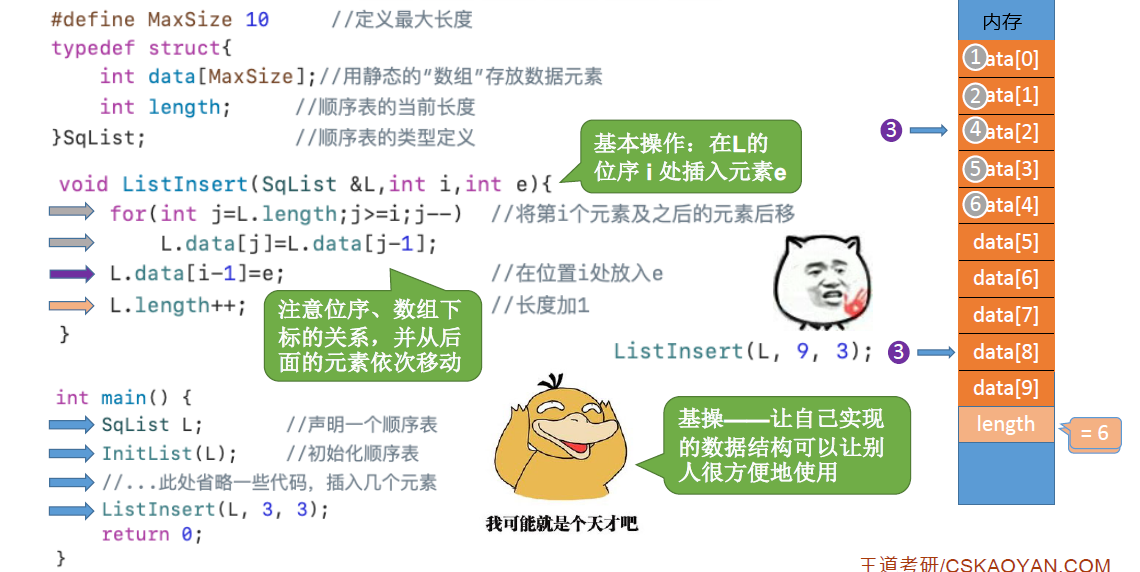
image-20220624174423967

增加i的合法性判断：

image-20220624174759948

顺序表的基本操作-删除：

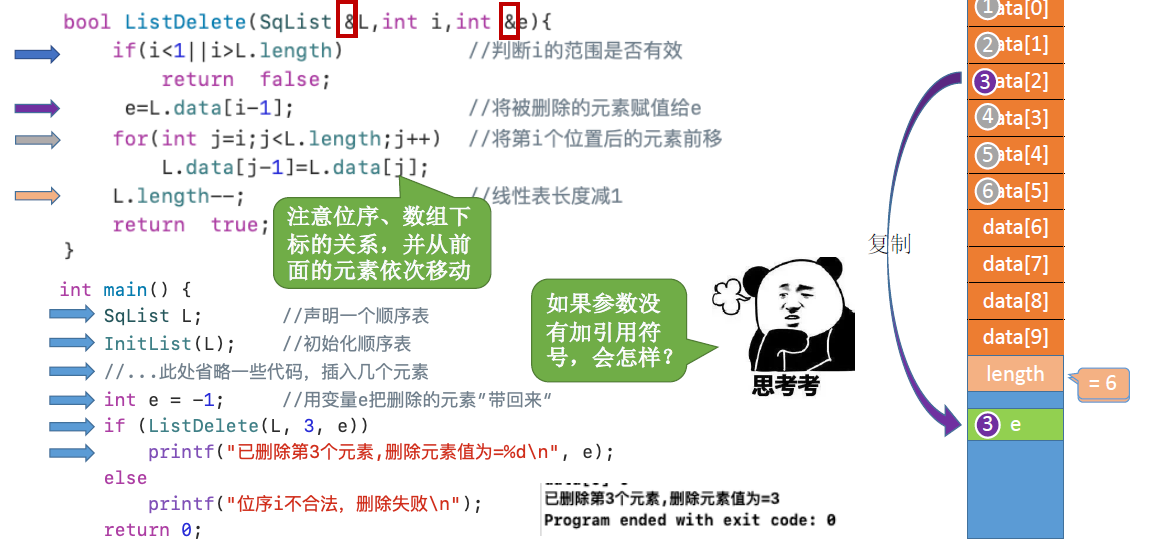
image-20220624175336716

插入和删除的时间复杂度：

  • 最好时间复杂度= O(1)
  • 最坏时间复杂度= O(n)
  • 平均时间复杂度= O(n)

顺序表的查找

顺序表的按位查找：

image-20220624203923807

  • 正是如此，在初始化顺序表时候malloc需要强制转换为与数据元素的数据类型相对应的指针
  • 时间复杂度= O(1)
  • 随机存取：由于顺序表的各个数据元素在内存中连续存放，因此可以根据起始地址和数据元素大小立即找到第i个元素，

顺序表的按值查找：

image-20220624204230030

  • 结构类型的数据元素也能用 == 比较吗：不能！（C++可以用 == 的重载来实现）
  • 更好的办法：定义一个函数
  • 依次对比各个分量来判断两个结构体是否相等
  • 最好时间复杂度= O(1)
  • 最坏时间复杂度= O(n)
  • 平均时间复杂度= O(n)

单链表的定义

顺序表：

  • 每个结点中只存放数据元素
  • 优点：可随机存取，存储密度高
  • 缺点：要求大片连续空间，改变容量不方便

单链表：

  • 每个结点除了存放数据元素外，还要存储指向下一个结点的指针
  • 优点：不要求大片连续空间，改变容量方便
  • 缺点：不可随机存取，要耗费一定空间存放指针

定义一个单链表：

  • typedef关键字：数据类型重命名
    • typedef <数据类型> <别名>
    • typedef struct LNode LNode;
    • 之后可以用LNode代替struct LNode

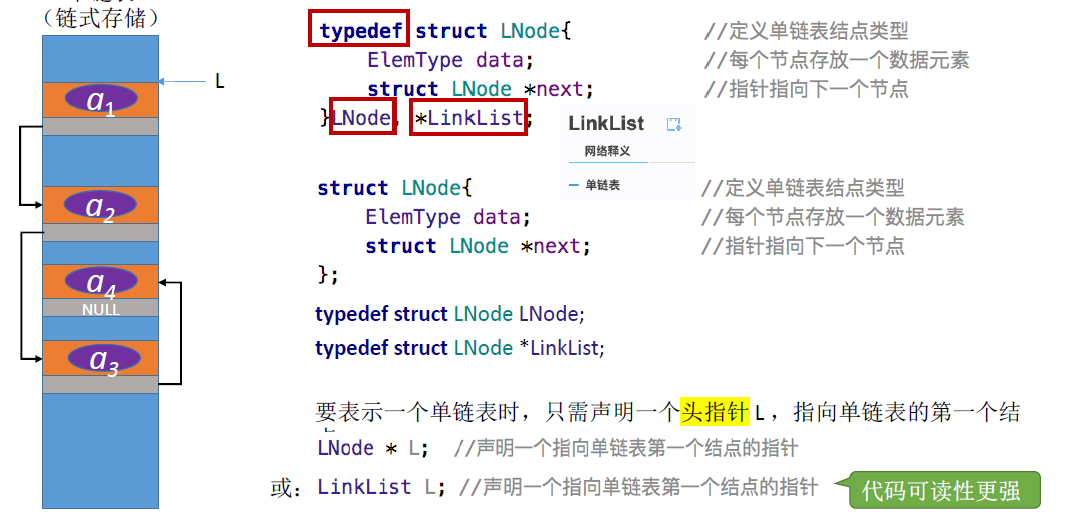
image-20220624223150765

image-20220624223324340

不带头结点的单链表：

image-20220624224456818

带头结点的单链表：

image-20220624224532853

区别：

  • 不带头结点，写代码更麻烦
  • 对第一个数据结点和后续数据结点的处理需要用不同的代码逻辑
  • 对空表和非空表的处理需要用不同的代码逻辑
  • 我们一般使用的都是带头结点的单链表

单链表的插入、删除

按位序插入（带头结点）：

ListInsert(&L,i,e)：

  • 插入操作，在表L中的第i个位置上插入指定元素e
  • 找到第i-1个结点，将新结点插入其后
  • 若带有头结点，插入更加方便，头结点可以看作“第0个”结点，直接做上面的操作即可

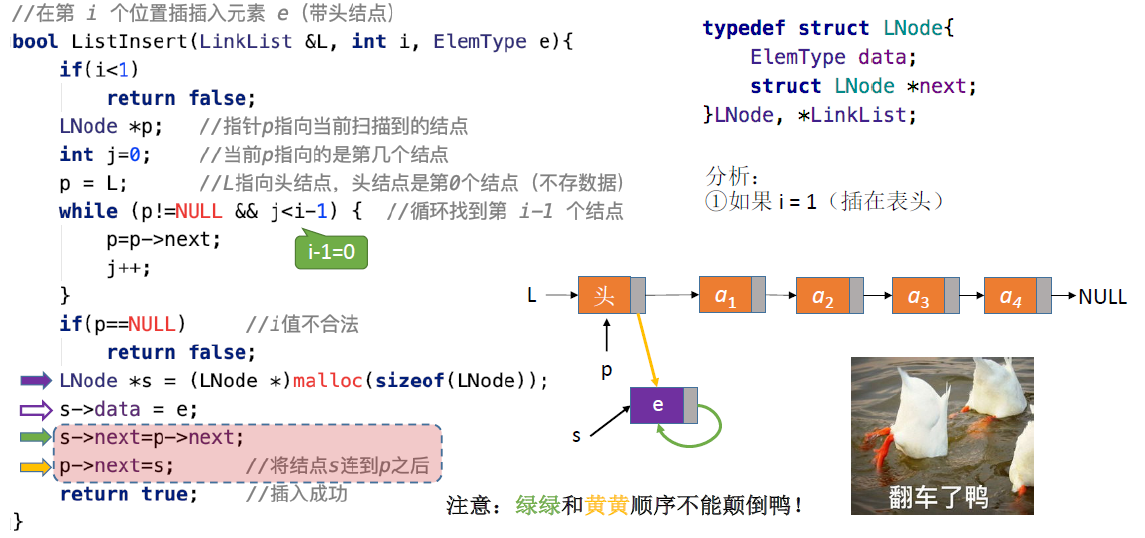
image-20220625002228781

  • 若i插在表中则与插在表头一样进行操作，可以插入成功
  • 若i插在表尾则s->next为NULL（在表的定义时规定的），可以插入成功
  • 若i插在表外（i>Lengh）则p指针指向NULL（While循环一直指向p->next），不能插入成功
  • 最好时间复杂度= O(1)
  • 最坏时间复杂度= O(n)
  • 平均时间复杂度= O(n)

按位序插入（不带头结点）：

ListInsert(&L,i,e)：

  • 插入操作，在表L中的第i个位置上插入指定元素e
  • 不存在“第0个”结点，因此i=1时需要特殊处理
  • 找到第i-1个结点，将新结点插入其后

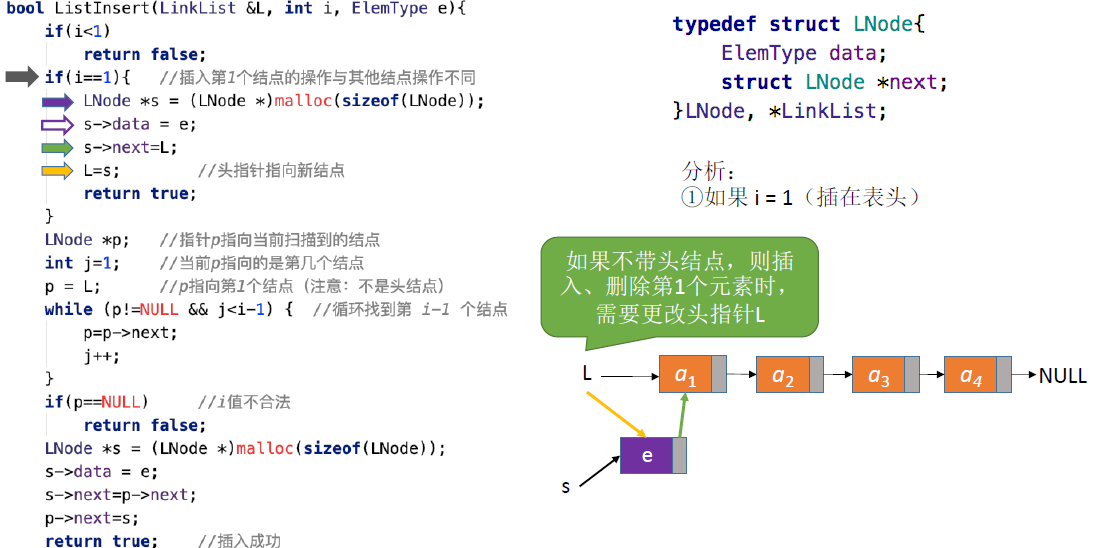
image-20220625003521556

  • 若i!=1则处理方法和带头结点一模一样
  • 值得注意的是int j =1而非带头结点的0（带头结点的头结点为第0个结点）
  • 结论：不带头结点写代码更不方便，推荐用带头结点

指定结点的后插操作：

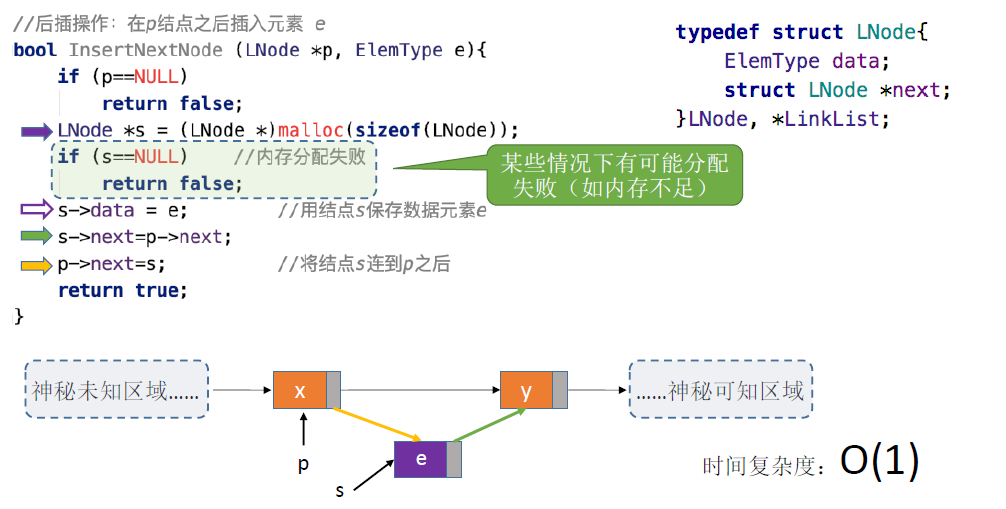
image-20220625004300810

  • 这一段代码是按位序插入中插入的那一部分代码
  • 也可以直接调用InsertNextNode来执行
  • 封装代码，以此提高代码复用性，让代码更容易维护

指定结点的前插操作：

  • 因为仅知道指定结点的信息和后继结点的指向，因此无法直接获取到前驱结点
  • 方法1：获取头结点然后再一步步找到指定结点的前驱
  • 方法2：将新结点先连上指定结点p的后继，接着指定结点p连上新结点s，将p中元素复制到s中，将p中元素覆盖为要插入的元素e

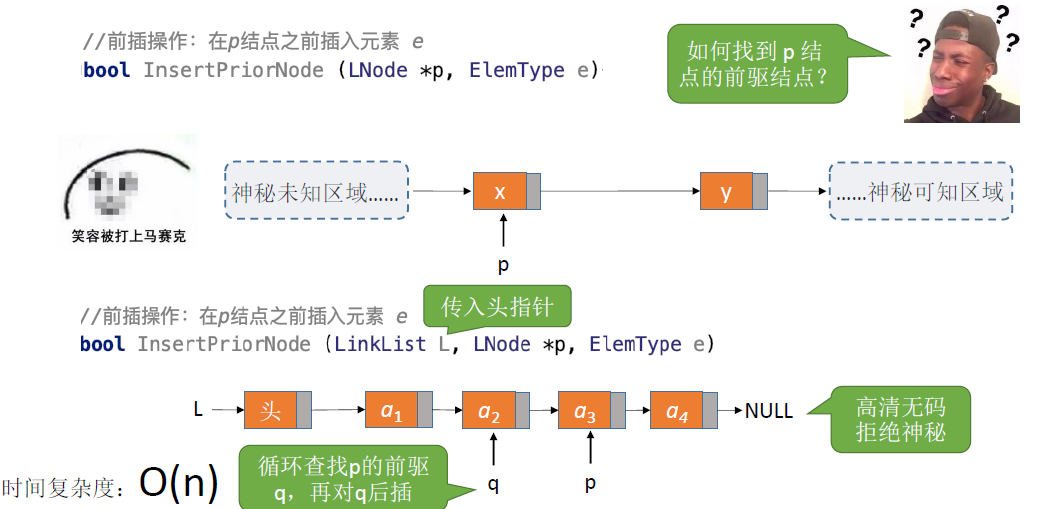image-20220625005533068 （方法1）

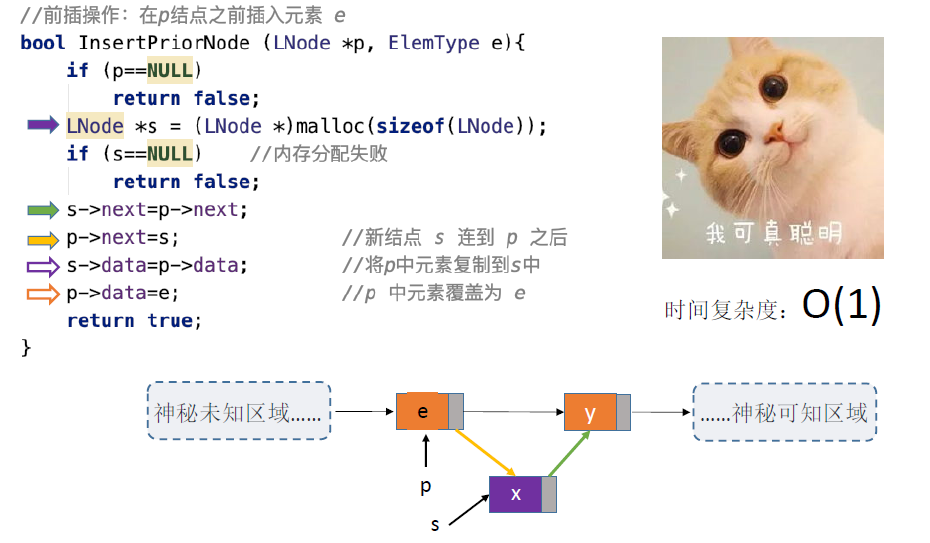image-20220625005516251 （方法2）

按位序删除（带头结点）：

ListDelete(&L,i,&e)：

  • 删除操作，删除表L中第i个位置的元素，并用e返回删除元素的值。
  • 找到第i-1个结点，将其指针指向第i+1个结点，并释放第i个结点

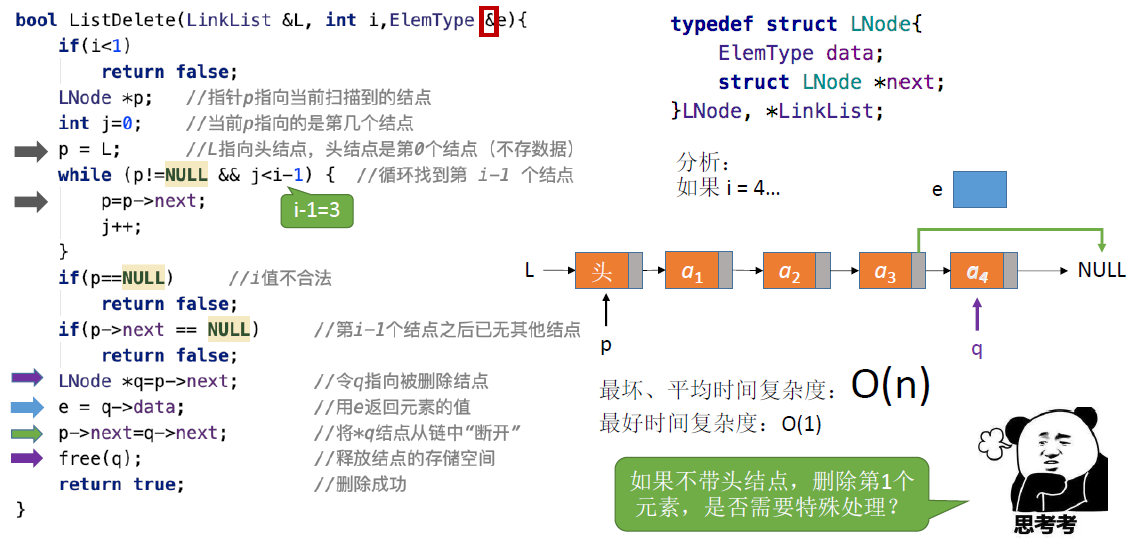
image-20220625010013814

指定结点的删除：

  • 删除结点p，需要修改其前驱结点的next指针，和指定结点的前插操作一样
  • 方法1：传入头指针，循环寻找p的前驱结点
  • 方法2：偷天换日，类似于结点前插的实现

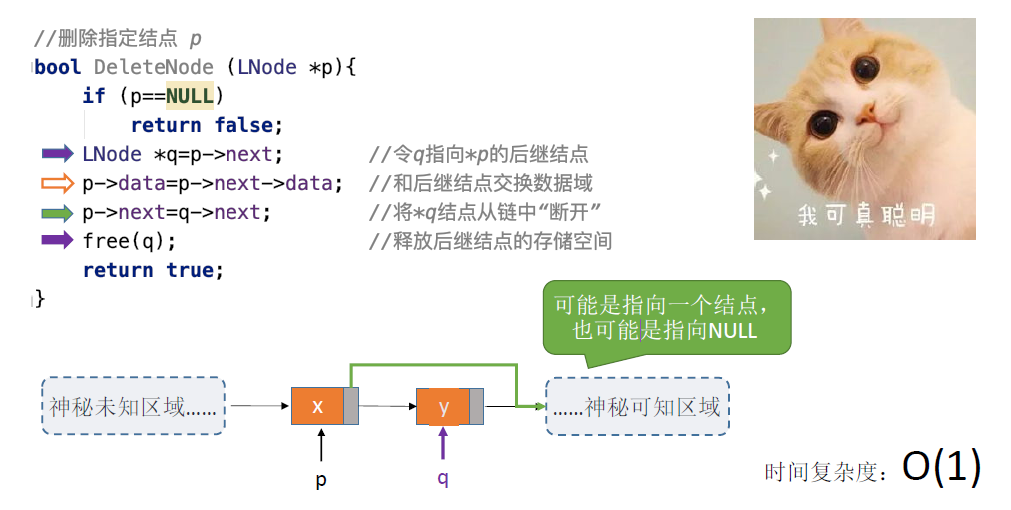image-20220625010204823 （方法2）

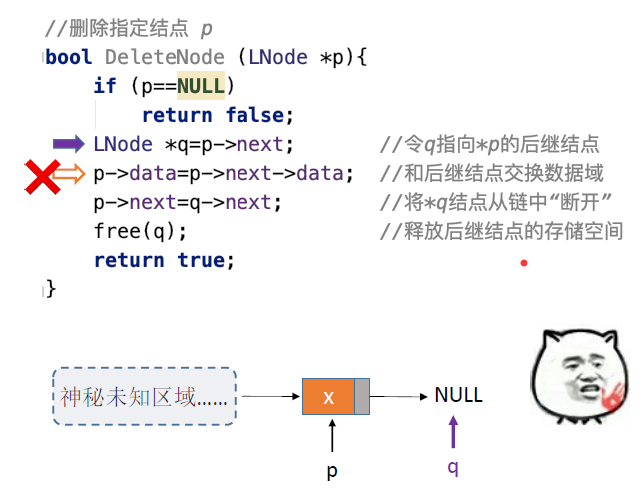
如果要删除的结点p是最后一个结点：

  • 只能从表头开始依次寻找p的前驱，时间复杂度O(n)
  • 这就体现了单链表的局限性：无法逆向检索，有时候不太方便

image-20220625010320242

单链表的查找

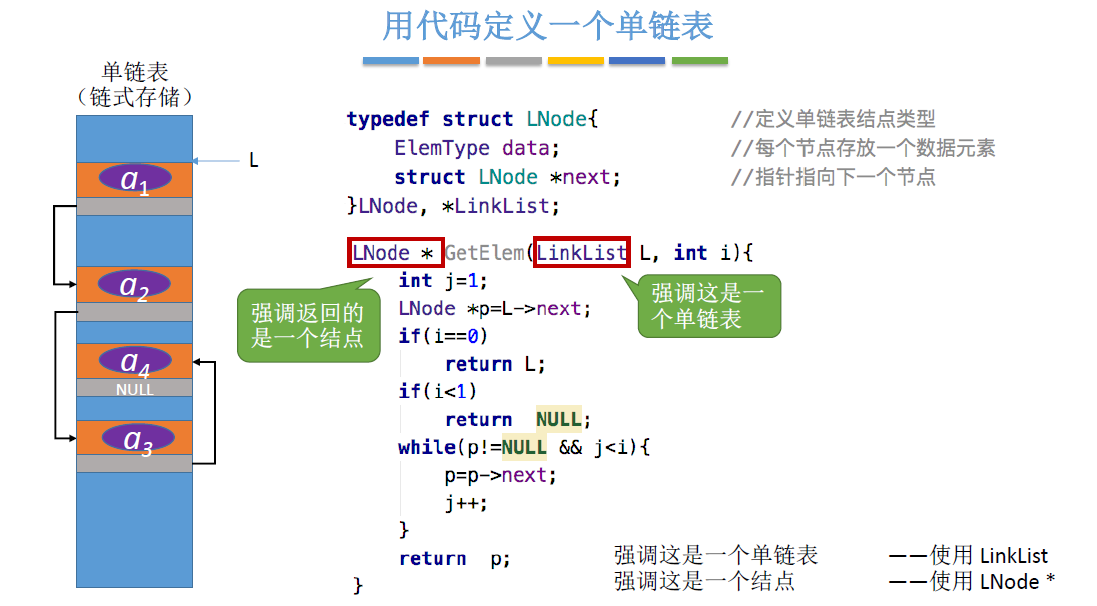
按位查找：

  • GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。
  • 实际上单链表的插入中找到i-1部分就是按位查找i-1个结点，如下图

image-20220625010645230

  • 因此查找第i个结点如下图

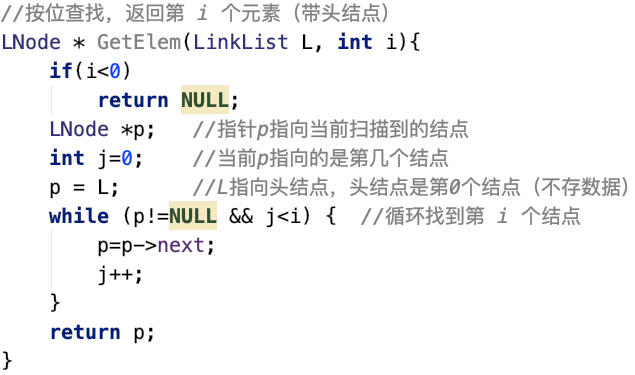
image-20220625014609795

  • 如果i=0则直接不满足j<i则指针p直接返回头结点L
  • 如果i超界则当时p指向了NULL，指针p返回NULL
  • 平均时间复杂度：O(n)

按值查找：

  • LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。

image-20220625015355288

  • 能找到的情况：p指向了e值对应的元素，返回该元素
  • 不能找到的情况：p指向了NULL，指针p返回NULL
  • 平均时间复杂度：O(n)

求表的长度：

image-20220625015647858

平均时间复杂度：O(n)

单链表的建立

尾插法：

  • 每次插入元素都插入到单链表的表尾
  • 方法1：套用之前学过的位序插入，每次都要从头开始往后面遍历，时间复杂度为O(n^2)

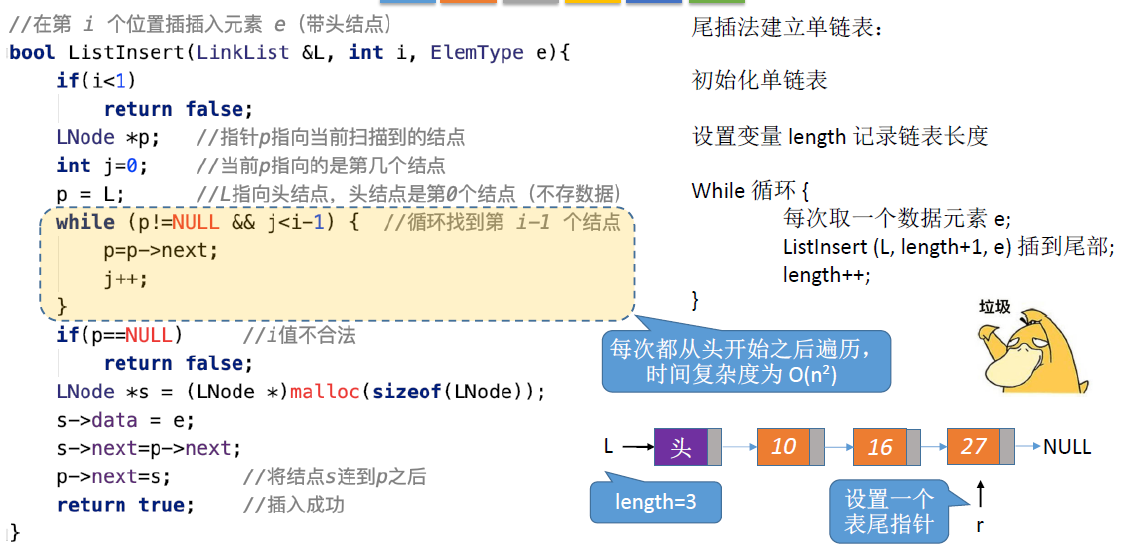
image-20220625143427581

  • 方法2：增加一个尾指针r，每次插入都让r指向新的表尾结点，时间复杂度为O(n)

image-20220625144158018

头插法：

  • 每次插入元素都插入到单链表的表头
  • 头插法和之前学过的单链表后插操作是一样的，可以直接套用
  • L->next=NULL;可以防止野指针

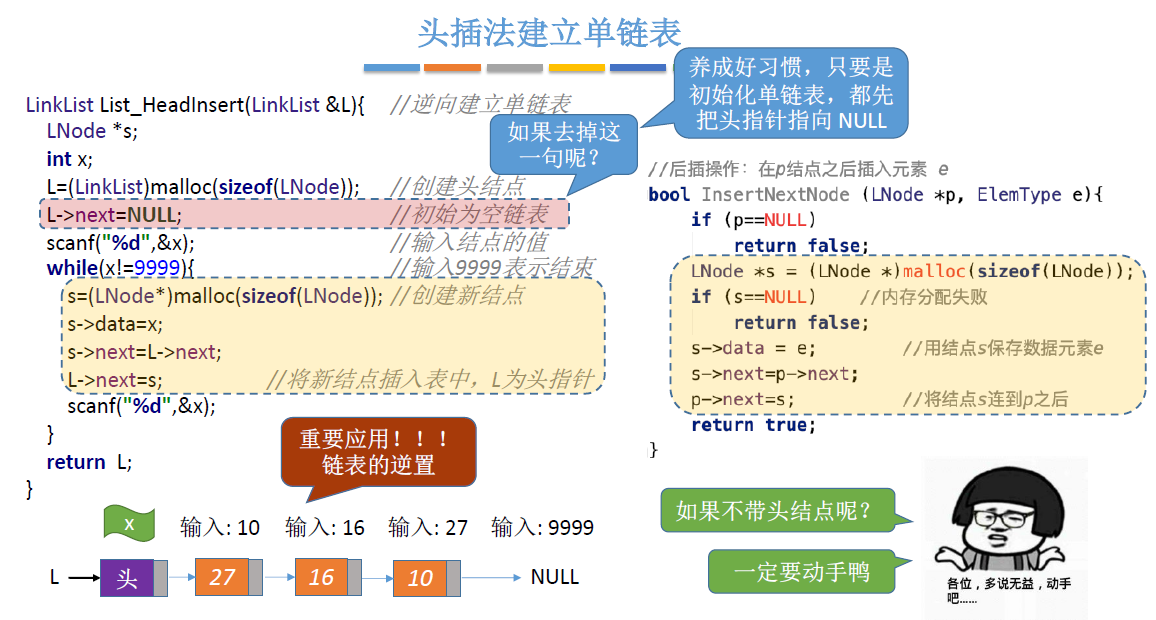
image-20220625144741628

总结：

  • 头插法、尾插法：核心就是初始化操作、指定结点的后插操作
  • 注意设置一个指向表尾结点的指针
  • 头插法的重要应用：链表的逆置

双链表

为什么要要使用双链表：

  • 单链表：无法逆向检索，有时候不太方便
  • 双链表：可进可退，但是存储密度更低一丢丢

image-20220625145549917

双链表的初始化（带头结点）：

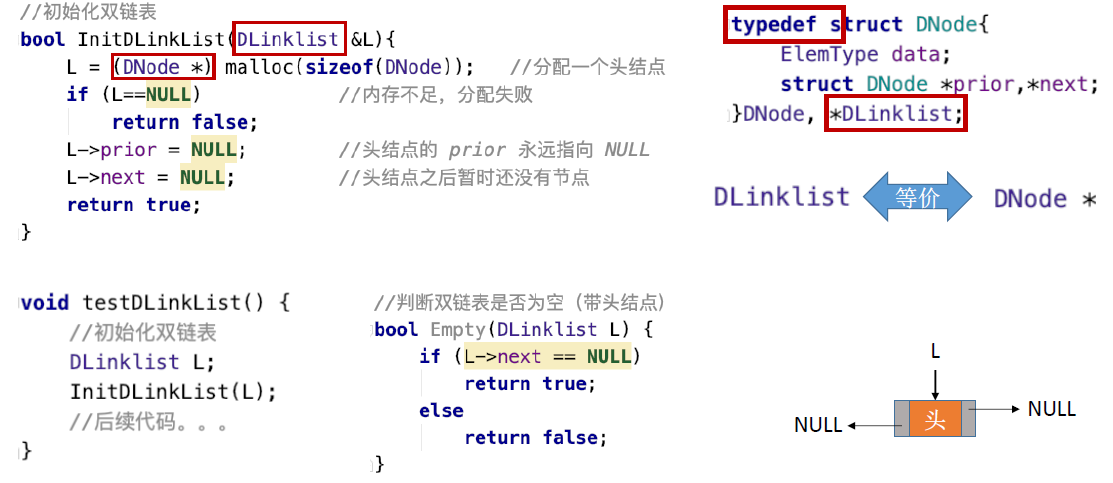
image-20220625145700963

双链表的插入：

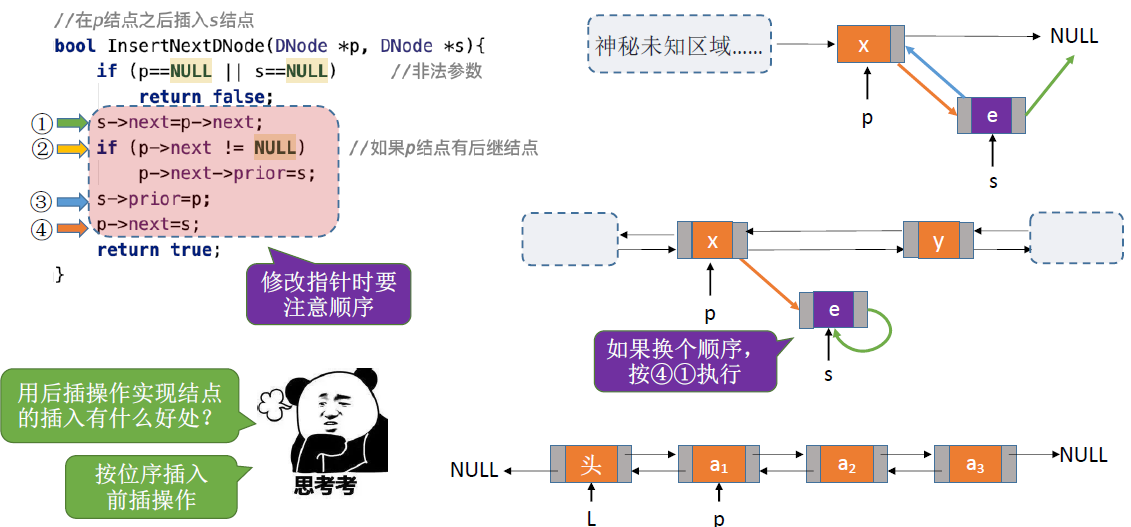
image-20220625150534610

  • 小心如果p结点为最后一个结点产生的空指针问题，因此循环链表应运而生（详见后面的循环链表插入删除）
  • 注意指针的修改顺序

双链表的删除：

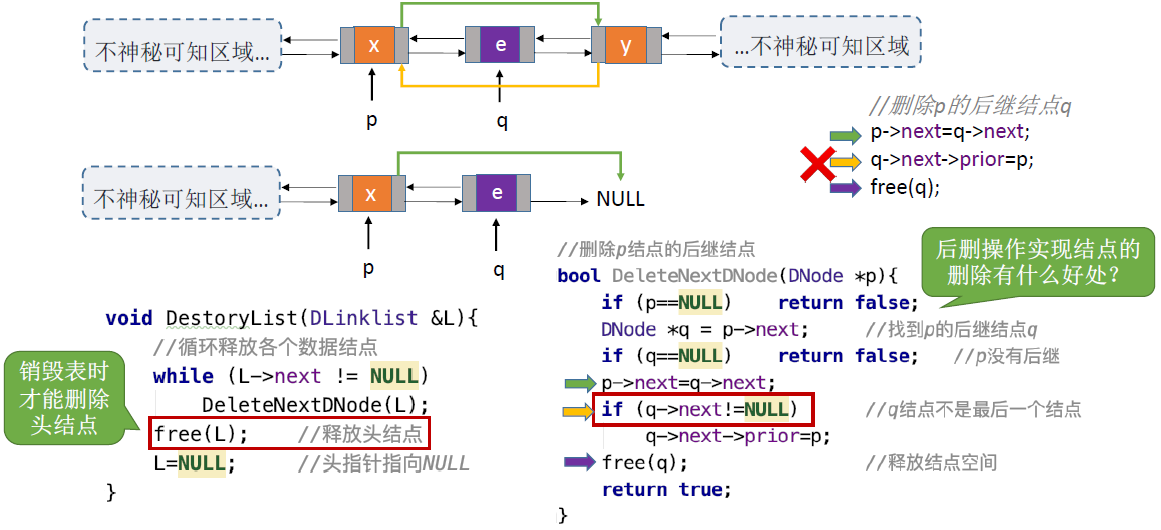
image-20220625150642007

双链表的遍历：

image-20220625150703796

循环链表

循环单链表与单链表的区别：

单链表：

  • 表尾结点的next指针指向NULL
  • 从一个结点出发只能找到后续的各个结点

循环单链表：

  • 表尾结点的next指针指向头结点
  • 从一个结点出发可以找到其他任何一个结点

循环单链表初始化：

image-20220627003508237

  • 从头结点找到尾部，时间复杂度为O(n)
  • 如果需要频繁的访问表头、表尾，可以让L指向表尾元素（插入、删除时可能需要修改L）
  • 从尾部找到头部，时间复杂度为O(1)

循环双链表与双链表的区别：

双链表：

  • 表头结点的prior指向NULL
  • 表尾结点的next指向NULL

循环双链表：

  • 表头结点的prior指向表尾结点
  • 表尾结点的next指向头结点

循环双链表的初始化：

image-20220627004314677

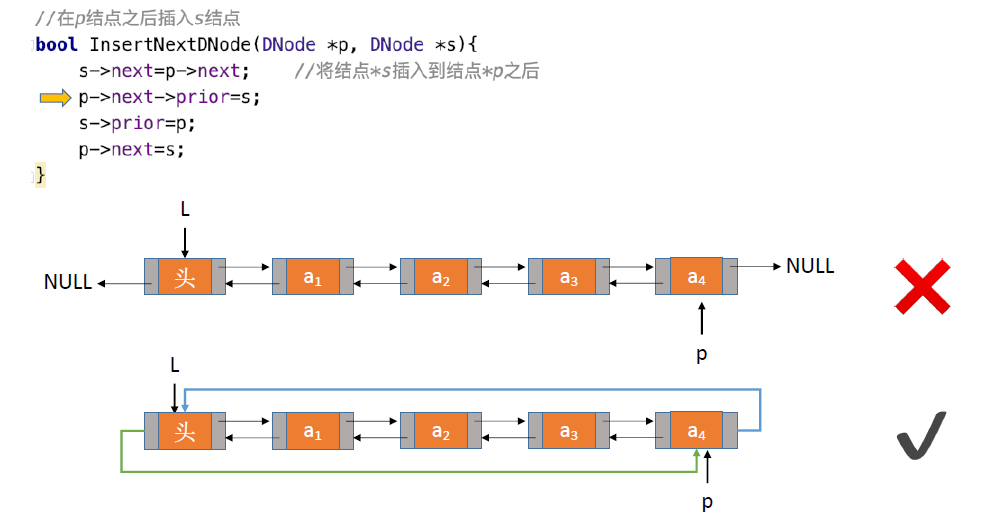
循环链表的插入：

  • 对于双链表来说如果p结点为最后一个结点，因为next结点为null，p->next->prior=s会产生的空指针问题
  • 循环链表规避因为最后结点的next结点为头结点因此不会发生问题

image-20220627004443320

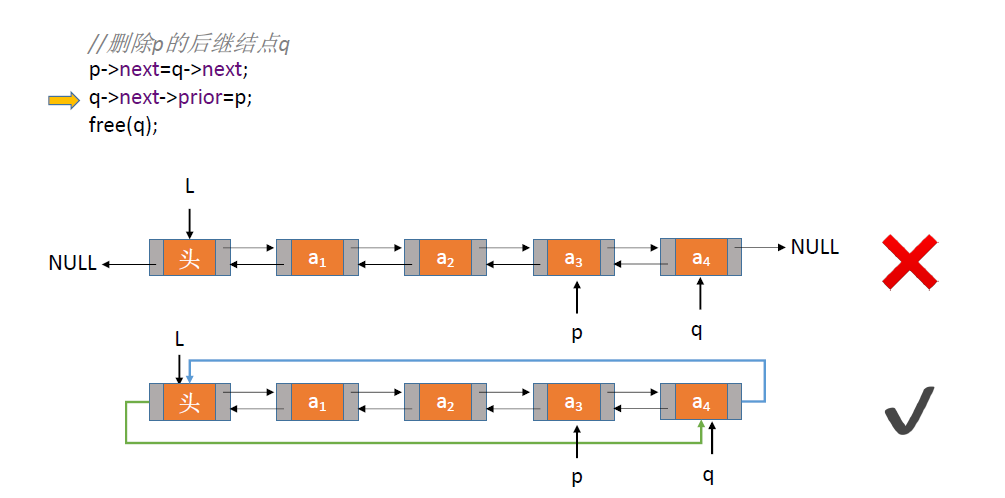
循环链表的删除：

与循环链表的插入相同。

image-20220627004747085

注意点：

写代码时候注意以下几点，以此规避错误：

  • 如何判空
  • 如何判断结点p是否是表尾/表头元素（后向/前向遍历的实现核心）
  • 如何在表头、表中、表尾插入/删除一个结点

静态链表

什么是静态链表：

  • 分配一整片连续的内存空间，各个结点集中安置
  • 每个结点由两部分组成：data（数据元素）和next（游标）
  • 0号结点充当“头结点”，不具体存放数据
  • 游标为-1表示已经到达表尾
  • 游标充当“指针”，表示下个结点的存放位置，下面举一个例子：
  • 每个数据元素4B，每个游标4B（每个结点共8B），设起始地址为addr，e1的存放地址为addr + 8*2（游标值）

定义静态链表：

方法1：

image-20220627005939769

方法2：

image-20220627010315615

基本操作：

初始化：

  • 把a[0]的next设为-1
  • 把其他结点的next设为一个特殊值用来表示结点空闲，如-2

插入位序为i的结点：

  • 找到一个空的结点，存入数据元素（设为一个特殊值用来表示结点空闲，如-2）
  • 从头结点出发找到位序为i-1的结点
  • 修改新结点的next
  • 修改i-1号结点的next

删除某个结点：

  • 从头结点出发找到前驱结点
  • 修改前驱结点的游标
  • 被删除结点next设为-2

总结：

  • 静态链表：用数组的方式实现的链表
  • 优点：增、删操作不需要大量移动元素
  • 缺点：不能随机存取，只能从头结点开始依次往后查找；容量固定不可变
  • 适用场景：①不支持指针的低级语言；②数据元素数量固定不变的场景（如操作系统的文件分配表FAT）

顺序表和链表的比较

逻辑结构：

都属于线性表，都是线性结构

存储结构：

顺序表：

  • 优点：支持随机存取、存储密度高
  • 缺点：大片连续空间分配不方便，改变容量不方便

链表：

  • 优点：离散的小空间分配方便，改变容量方便
  • 缺点：不可随机存取，存储密度低

基本操作：

顺序表：

  • 创建
    • 需要预分配大片连续空间。
    • 若分配空间过小，则之后不方便拓展容量；
    • 若分配空间过大，则浪费内存资源
    • 静态分配：静态数组实现，容量不可改变
    • 动态分配：动态数组（malloc、free）实现，容量可以改变但需要移动大量元素，时间代价高
  • 销毁
    • 修改Length = 0
    • 静态分配：静态数组，系统自动回收空间
    • 动态分配：动态数组（malloc、free），需要手动free
  • 增删
    • 插入/删除元素要将后续元素都后移/前移
    • 时间复杂度O(n)，时间开销主要来自移动元素
    • 若数据元素很大，则移动的时间代价很高
  • 查
    • 按位查找：O(1)
    • 按值查找：O(n)若表内元素有序，可在O(log2n)时间内找到

链表：

  • 创建
    • 只需分配一个头结点（也可以不要头结点，只声明一个头指针），之后方便拓展
  • 销毁
    • 依次删除各个结点（free）
  • 增删
    • 插入/删除元素只需修改指针即可
    • 时间复杂度O(n)，时间开销主要来自查找目标元素
    • 查找元素的时间代价更低
  • 查
    • 按位查找：O(n)
    • 按值查找：O(n)

用哪个：

  • 表长难以预估、经常要增加/删除元素——链表
  • 表长可预估、查询（搜索）操作较多——顺序表

开放式问题的解题思路：

问题： 请描述顺序表和链表的bla bla bla…实现线性表时，用顺序表还是链表好？

答案：

  • 顺序表和链表的逻辑结构都是线性结构，都属于线性表。
  • 但是二者的存储结构不同，顺序表采用顺序存储…(特点，带来的优点缺点)；链表采用链式存储…（特点、导致的优缺点）。
  • 由于采用不同的存储方式实现，因此基本操作的实现效率也不同。
  • 当初始化时…；当插入一个数据元素时…；当删除一个数据元素时…；当查找一个数据元素时…

笔记完整PDF

百度网盘提取码：l3ja

赏