目录
着色
定义:对不同的物体应用不同的材质
Blinn-Phong反射模型
裴祥风(Bùi Tường Phong)先生改进的反射模型。
- 高光(Specular highlights)
- 漫反射(Diffuse reflection)
- 间接/环境光照(Ambient lighting)
漫反射
兰伯特余弦定律(Lambert)
兰伯特余弦定律:cosθ=l·n
n:法线方向
l:光照方向
不同角度的物体反射的光不同
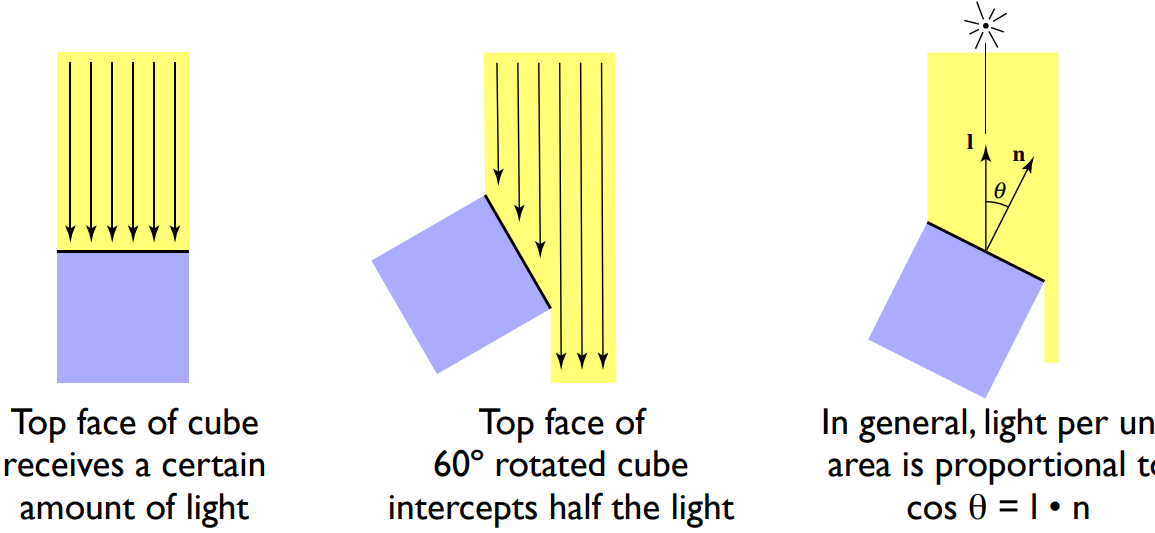
光照衰减
I1=I0/r²
I:光线强度
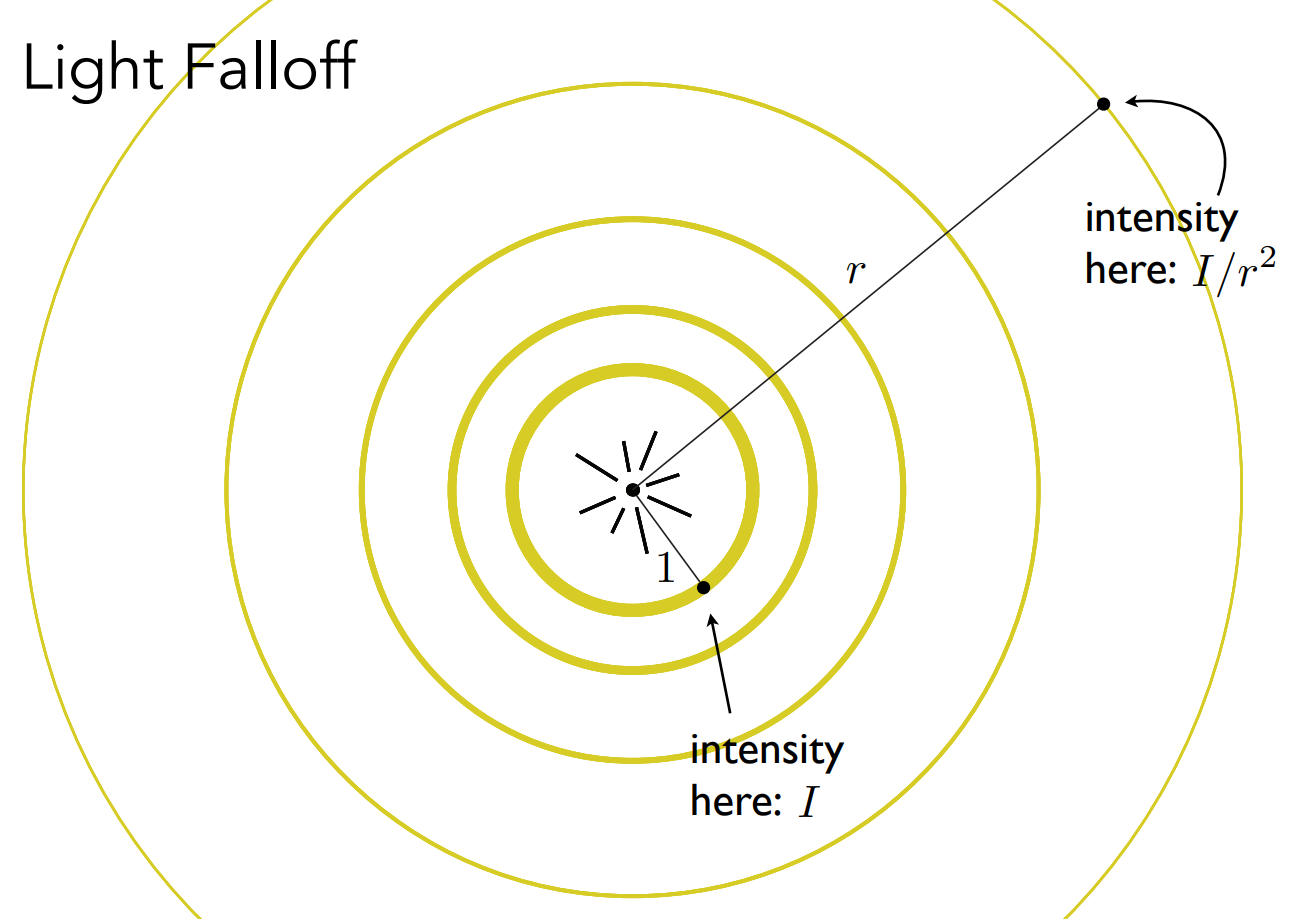
朗伯着色器
Kd:颜色扩散系数
Ld:漫反射反射光
漫反射只和物体本身与光线有关,与观察方向v无关
引入max(0,n·l)是因为若点乘小于0说明是从下面射过来的,没有意义。
若两个向量的点乘接近1则离得很近,若接近0则离得很远。
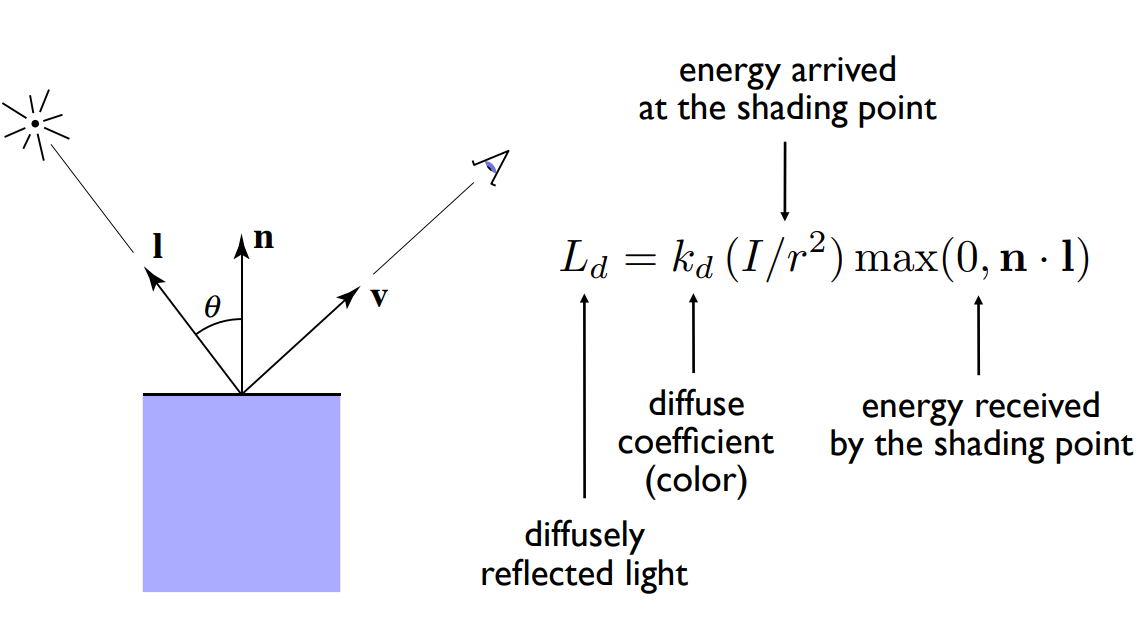
高光
Ls:高光反射光
Ks:镜面反射系数(通常认为是白色的)
引入半程向量h,如果镜面反射方向与观察点接近,则半程向量h与法线方向n接近
Blinn-Phong反射模型是对Phong反射模型得改进,引入半程向量h比使用镜面反射方向r计算量更小
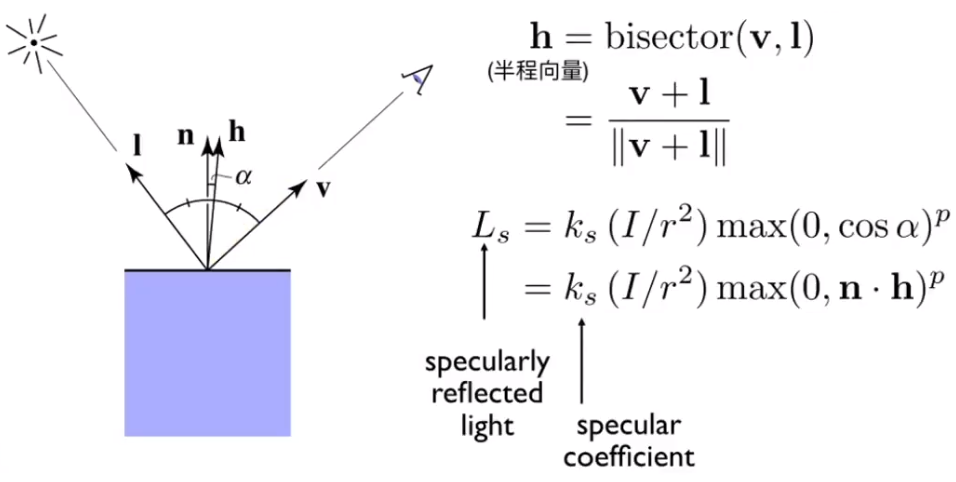
由于cosα的容忍度太大,导致高光太大,所以引入p次幂,一般使用100-200次幂
环境光照

环境光与入射方向、法线方向、观察方向无关,是一个常数
总结
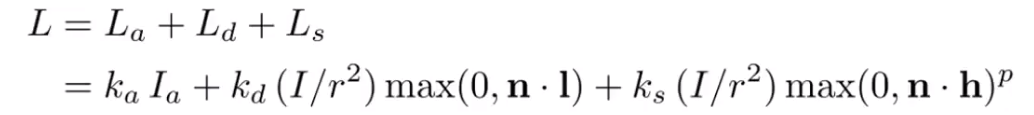
着色频率
着色频率不同,着色效果也不同
- 以顶点为单位着色(Gouraud shading)
- 以三角形平面为单位着色(Flat shading)
- 以像素为单位着色(Phong shading)
如果面足够多,逐顶点未必比逐像素效果好。
从一个球来获取法线方向是容易的,
复杂的模型通过将相邻的四个面进行对面积的加权平均得到四个面的平均法向量。
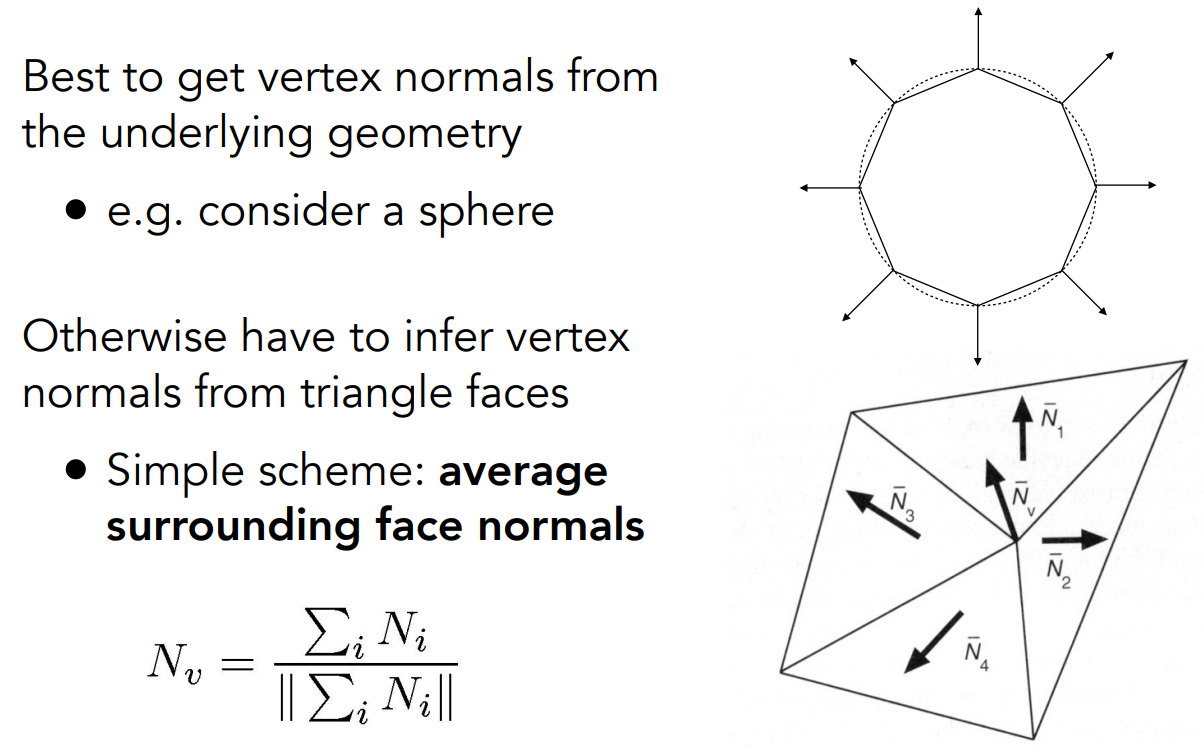
逐像素着色通过顶点法线的重心插值来实现
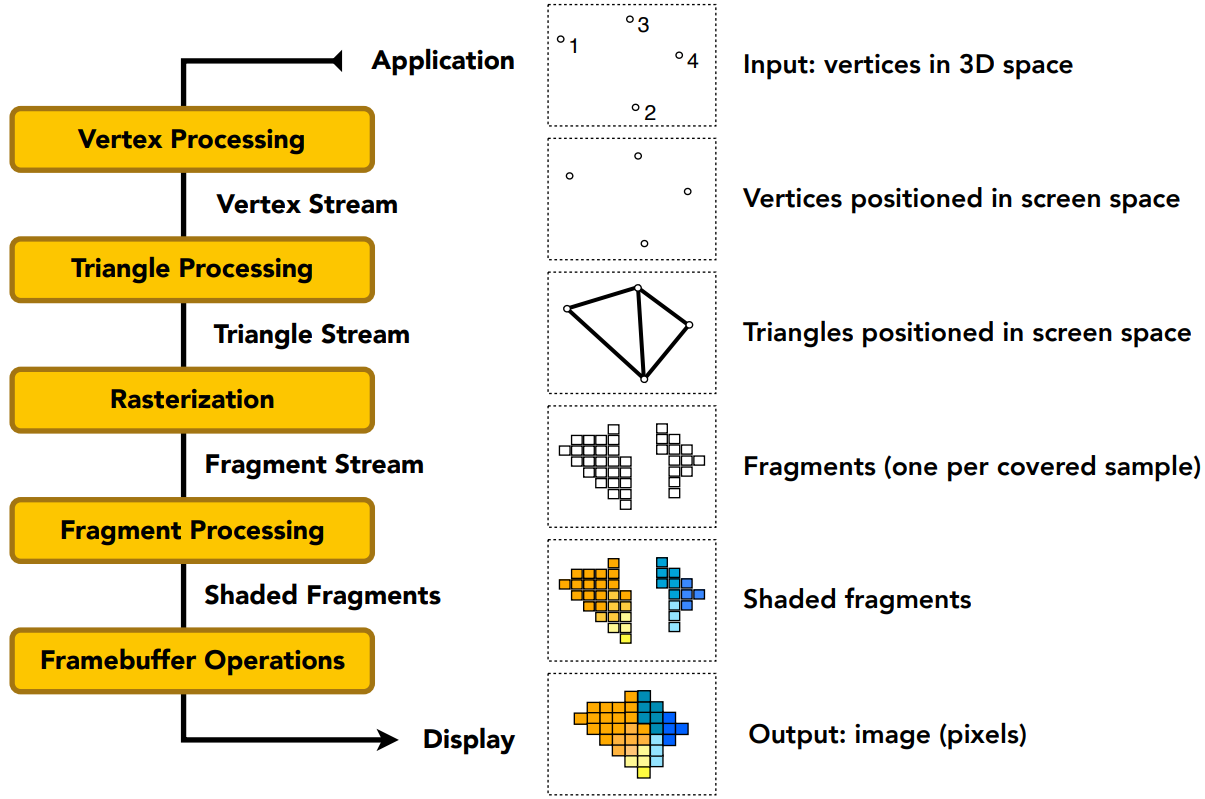
实时渲染管线
简化的流程
- 输入空间中一系列的点
- 顶点处理
- 三角形处理
- 光栅化
- 着色
- 片段(像素)处理
- 帧缓冲区处理
- 输出
目前渲染管线都是在GPU中被编程完成了,只有顶点处理和片段处理可以编程
Shader编程
利用GLSL对顶点着色器和片段着色器进行编程。
片段着色器对每个片段都执行一次。
以下是一个GLSL片段着色器的程序代码:
uniform sampler2D myTexture; // 获取纹理 uniform是全局变量
uniform vec3 lightDir; //获取光照方向
varying vec2 uv;//获取uv坐标
varying vec3 norm; //获取法线坐标
void diffuseShader()
{
vec3 kd;//获取kd系数
kd = texture2d(myTexture, uv);
kd *= clamp(dot(–lightDir, norm), 0.0, 1.0); //Phong模型漫反射
gl_FragColor = vec4(kd, 1.0); //输出该像素的颜色
}
图形管线实现工具
- 集成显卡
- 独立显卡
GPU:多核心进行多现成并行计算
纹理映射
纹理映射就是定义任意点的基本属性。
每个三维的模型上的任意点都能对应在uv坐标上的某个点上。
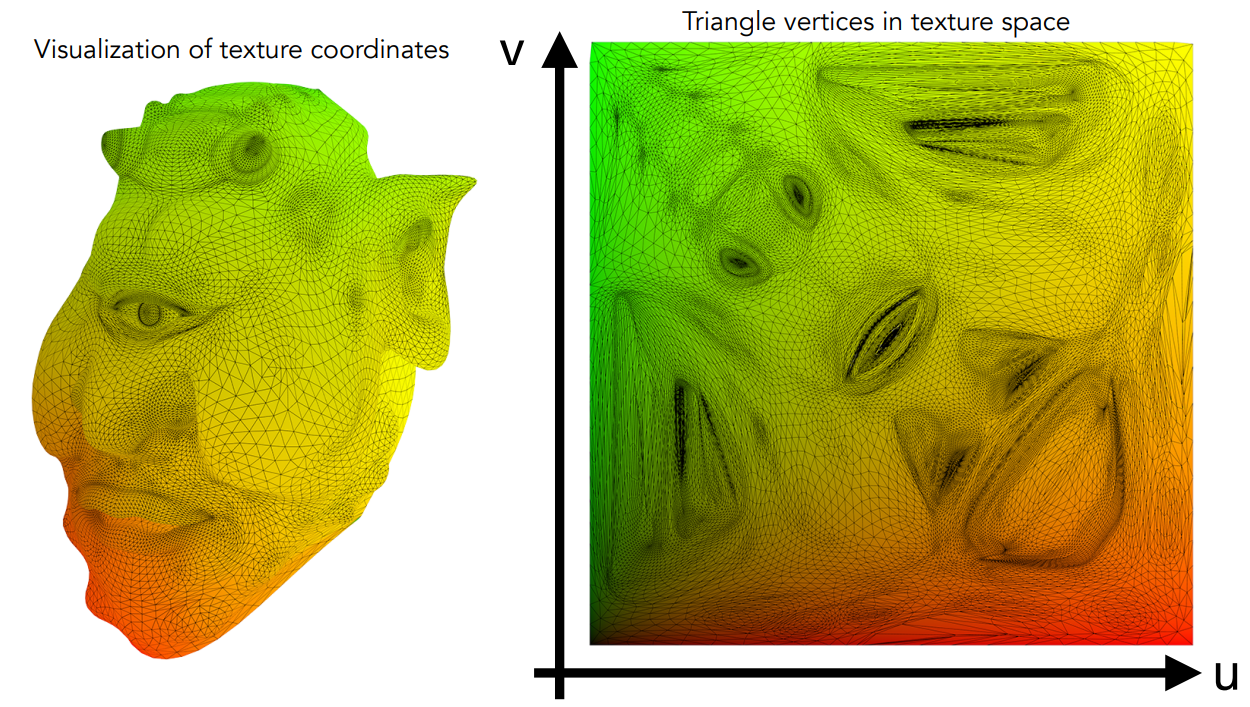
纹理可以被重复使用

重心坐标
插值
为什么要插值?
为了获取平滑的过渡
插值的内容有哪些?
纹理坐标、颜色、法向量
如何做插值?
定义与性质
重心坐标是定义在三角形上的,在三角形ABC所形成的平面内任意一个点(x,y)都可以表示为三个顶点ABC坐标的线性组合。
仅需要满足α+β+γ=1的条件。若αβγ均非负数,则(x,y)点一定在三角形内。
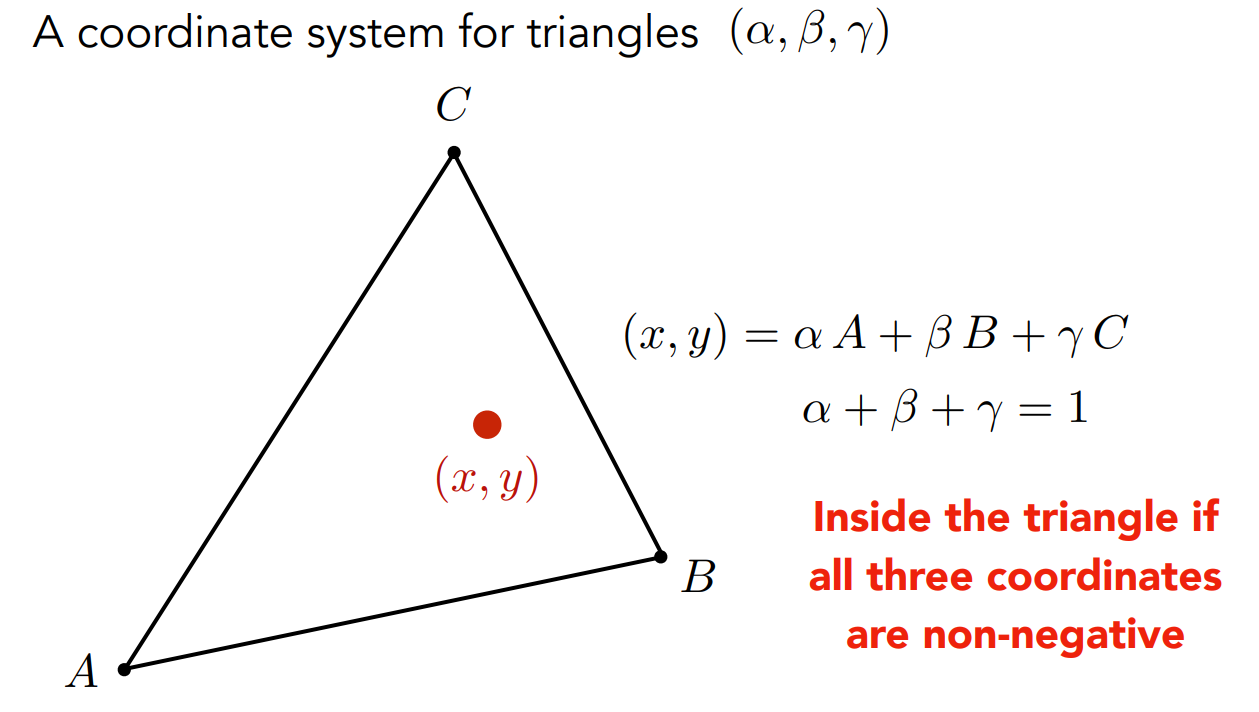
A点的重心坐标为(1,0,0)
B点为(0,1,0)
C点为(0,0,1)
同时,重心坐标的αβγ可以使用它占三角形的总面积来表示,
例如AA的面积为(x,y)点与BC点的连线形成的小三角形,
因此也说明了αβγ相加为什么需要等于1。
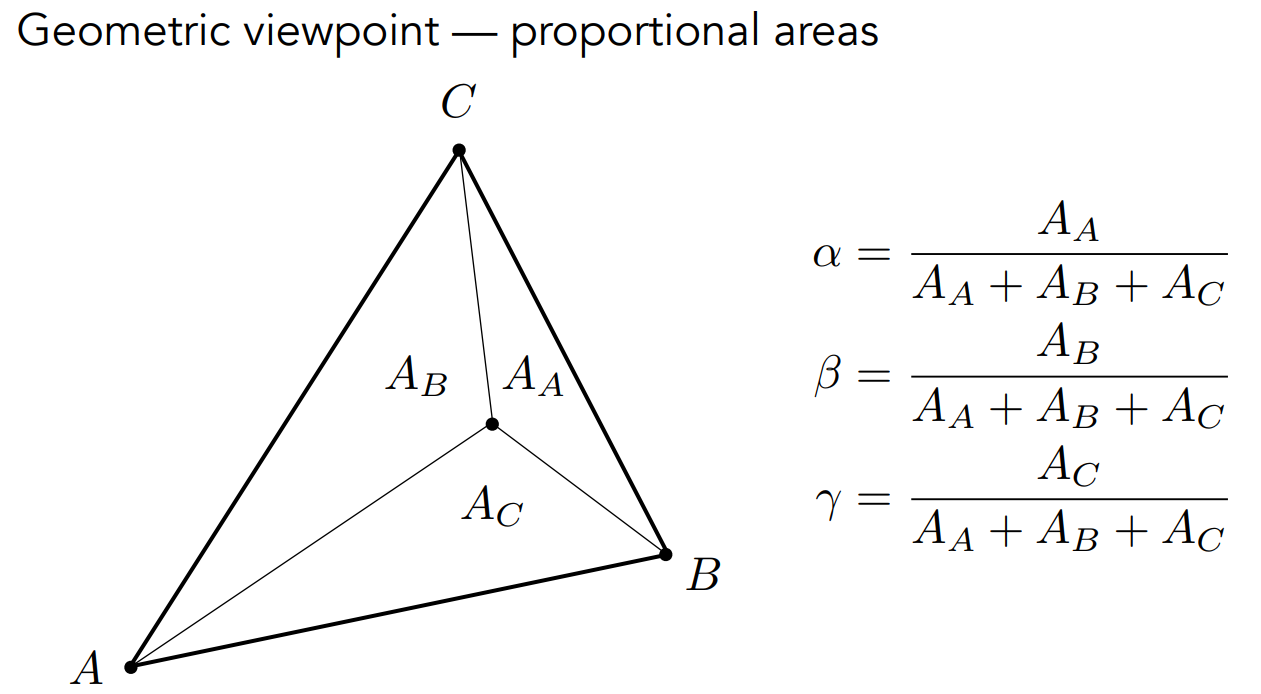
重心可以表示为(α,β,γ)=(1/3,1/3,1/3)
插值的应用
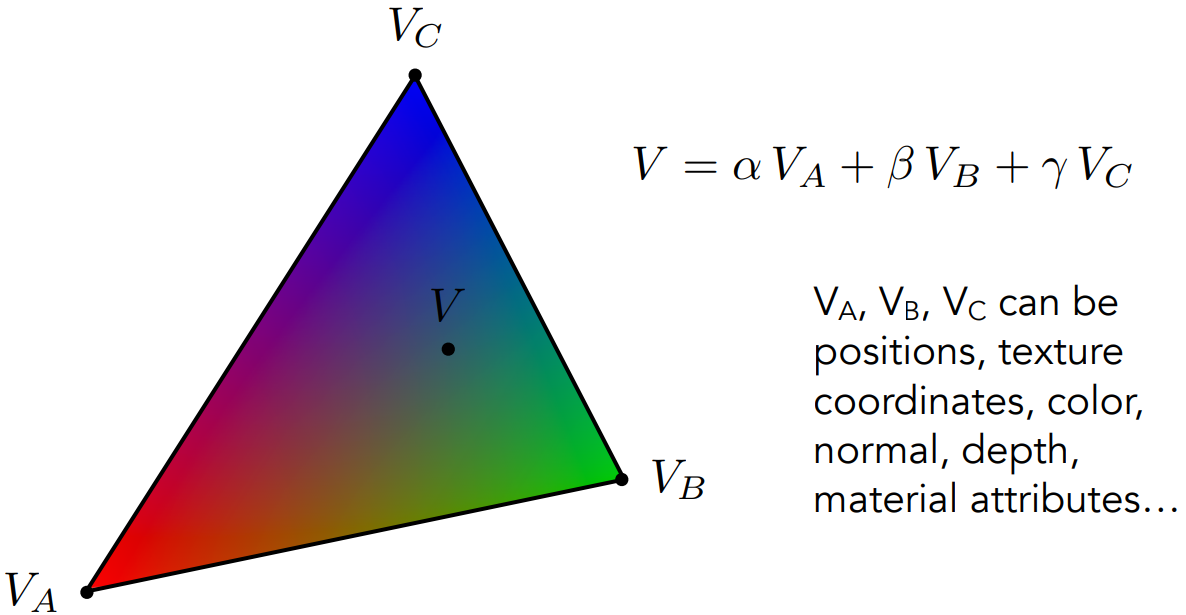
因此可以通过获得ABC点的值来获取到三角形内任意坐标的位置、颜色、法线、深度等信息。
值得注意的是在投影下不能保证坐标不变,所以要线插值再进行投影。
应用材质
将原本在各个顶点上的值,通过重心坐标插值到uv以及纹理坐标上的频幕上的每个采样点上。
纹理定义的值就是漫反射系数Kd
问题1:纹理太小了怎么办?-双线性插值

双线性插值(中)和双三线性插值(右)
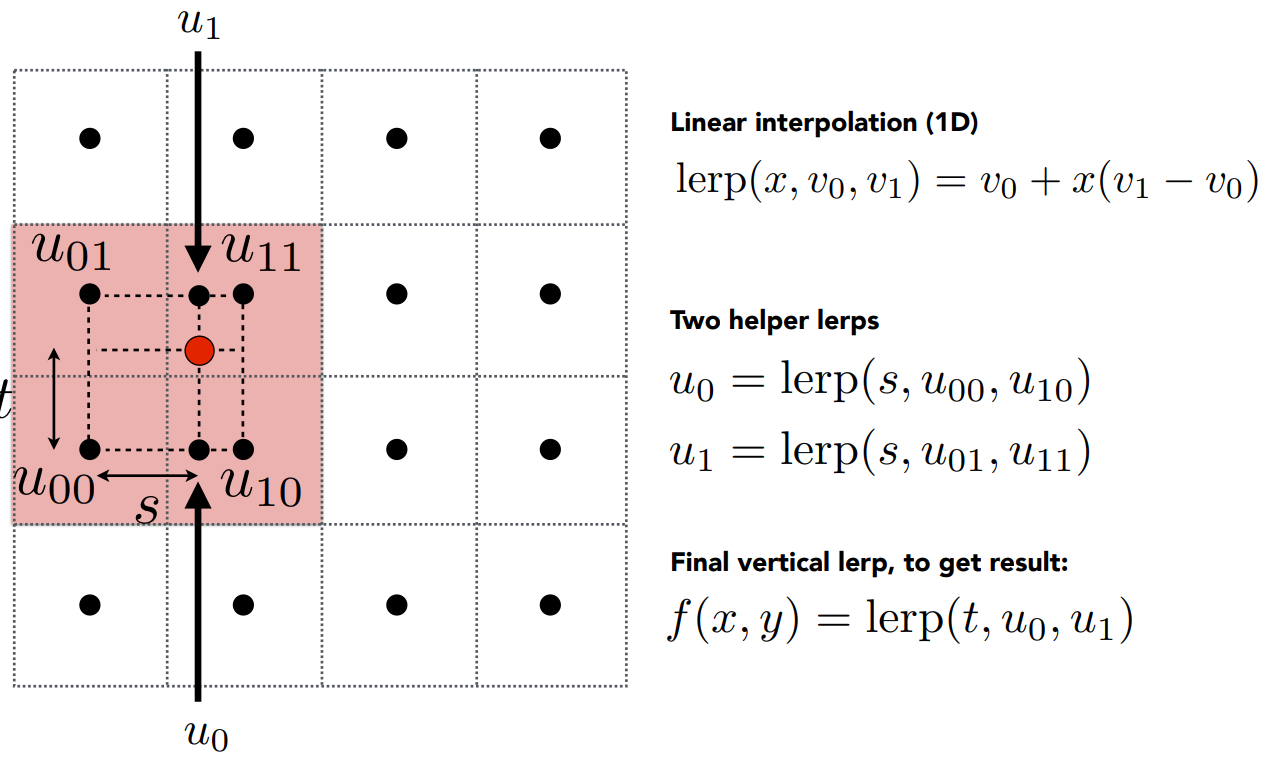
双线性插值(Bilinear)
- 找到(s,t),s、t都在0-1之间
- 进行线性插值
- 先进行上下两点的水平插值,例如u0 =(u00+u10)s
- 再进行竖直的插值(u0+u1)t
- 得到红点对应的值,例如rgb值
问题2:纹理太大怎么办?-Mipmap
会造成近处出现锯齿,远处出现摩尔纹。
Mipmap只能做近似的正方形的范围查询。

- level0是原始图像,每提高一个level,分辨率小一倍,利用相邻的四个像素的rgb做平均操作。
- 做mipmap比会增加原本图像1/3的额外存储量。
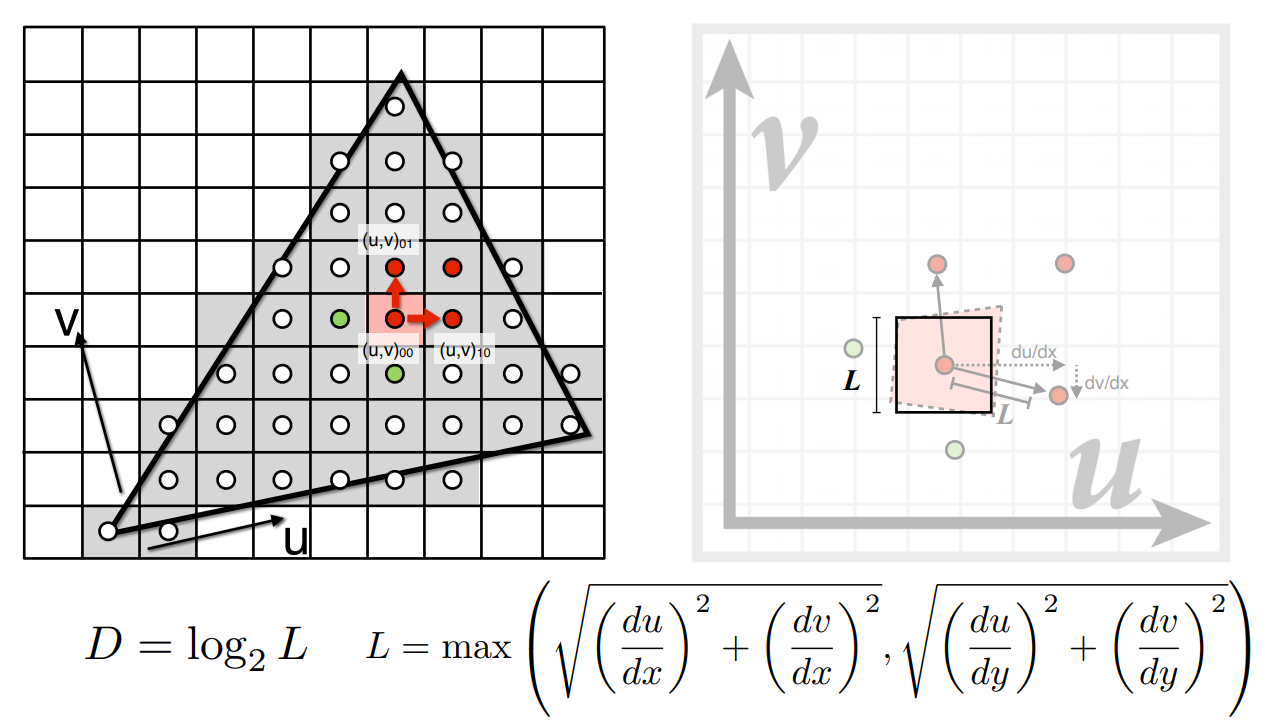
Mipmap操作:
- 在屏幕空间中取当前像素相邻的像素并查询其对应的uv坐标。
- 计算出当前像素点与其他像素点距离的最大值L。
- 根据最大值L通过上面公式计算得到该点所处的层数D。

通过mipmap操作得到哪些区域的像素要使用第几层进行平均操作。
过渡不平滑-三线性插值
如果算出来的D值是一个小数,这会造成图片Mipmap做错不平滑的问题。
如何解决——三线性插值
- 对该D值分别进行向下和向上取整。如D=1.2Z则取1和2
- 对两个D值分别进行双线性插值(见纹理太小)。
- 对两个插值的结果再做一次线性插值,如0.8xD1+0.2xD2

过度模糊-各向异性过滤

如果只使用Mipmap则远处会出现过度模糊的问题(完全糊成一块)。
如何解决——各向异性过滤
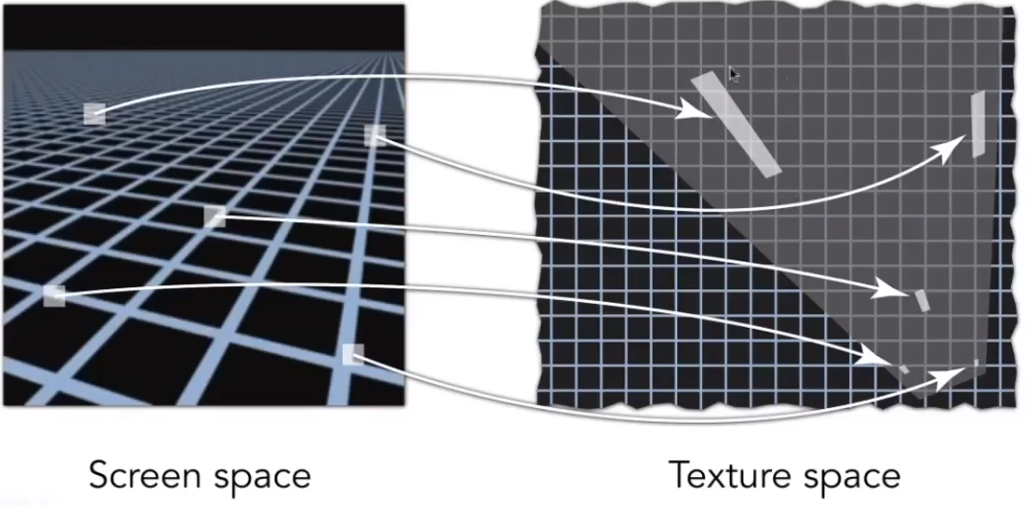
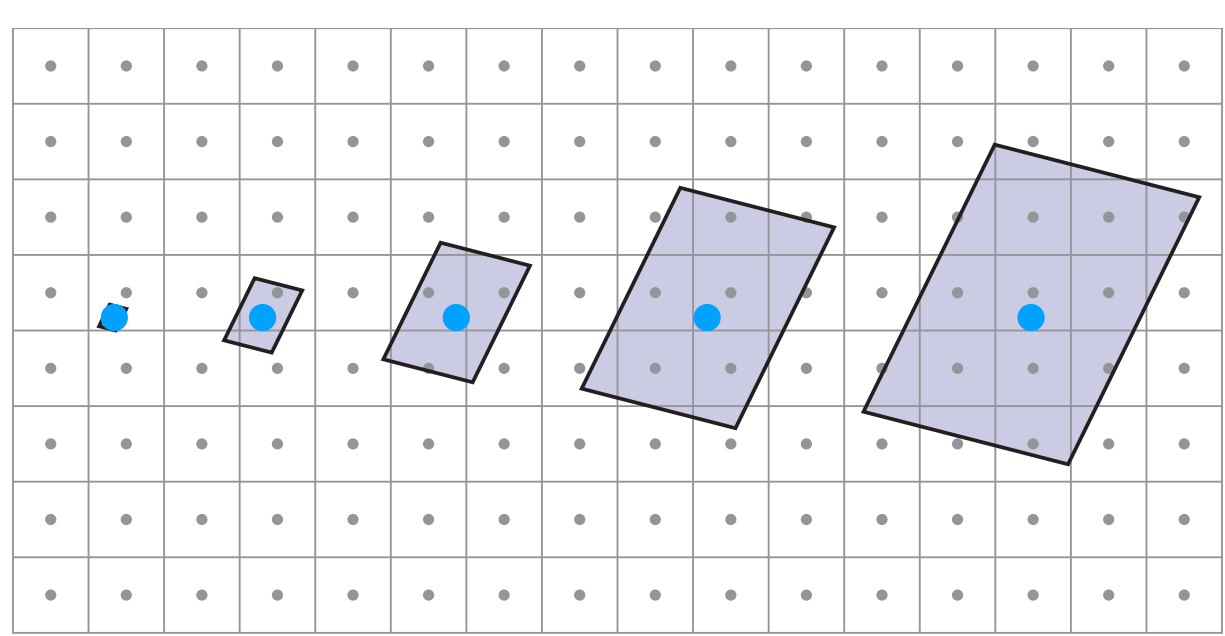
纹理中未必都是正方形的像素,因此运用mipmap查询会造成查询范围过大。

对矩形进行x轴或者y轴的压缩来进行各向异性过滤。
各项异性过滤可以解决矩形的纹理,但无法解决斜向的纹理。
解决斜向的纹理-EWA过滤。通过多次圆形的采样来解决过度模糊的问题。
纹理映射的应用
纹理=内存+范围查询(例如mipmap)
纹理是GPU上的一块内存,我们可以对内存做范围查询。
环境映射(Environment Map)
球面环境映射(Spherical Environment Map):
将环境光反射在球上就可以获得该场景的环境光。

球面映射(Spherical Map):
将球面环境映射可以展开为一张图,但是上下会被扭曲(类似世界地图)

立方体映射(CubeMap):
为了解决球面扭曲的问题,使用立方体来进行环境光照的纹理映射。

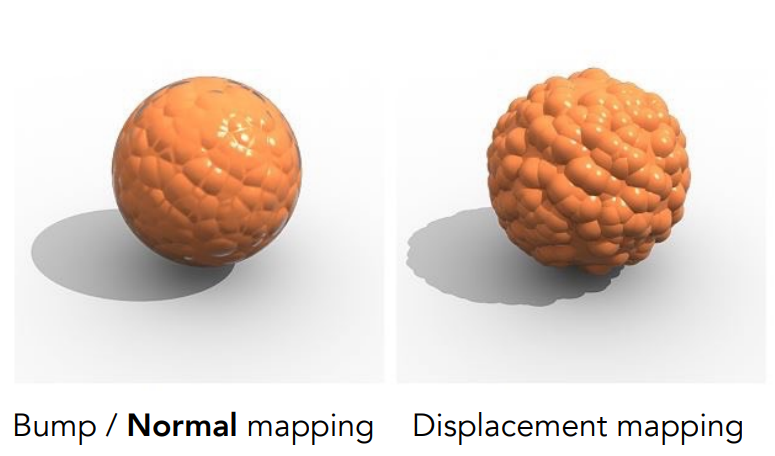
凹凸/法线贴图(Bump/Normal Map)
- 其最大的意义是为了表现相对高度来展示凹凸效果减少面数。
- 凹凸、法线贴图仅表示凹凸效果不会改变几何形体。
计算法线贴图(一维)
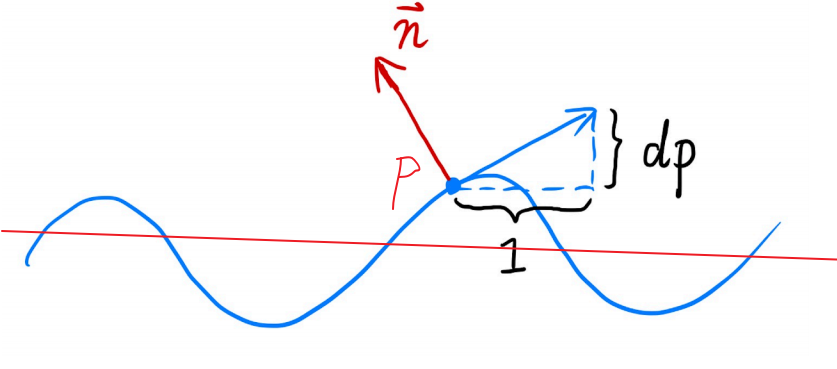
假设下图中的蓝点为p点()
- p点原来的法线朝上,即n(p) = (0, 1)
- 下图蓝色曲线为使用法线贴图后的效果。
- 通过dp = (c[h(p+1) - h(p)])/1求出两点的高度差。其中c为常数表示凹凸贴图的影响程度,h为高度p点、p+1点对应高度。
- 因此切线可表示为(1,dp)。
- 切线与法线为垂直的关系因此n(p) = (-dp, 1)
计算法线贴图(二维)
二维的情况下有u、v两个方向的变换。
实际情况下法线方向不一定朝上,这里的例子是基于一个局部坐标系确定的。
- n(p) = (0, 0,1)
- dp/du = c1 * [h(u+1) - h(u)]
- dp/dv = c2 * [h(v+1) - h(v)]
- n = (-dp/du, -dp/dv, 1)
位移贴图(Displacement mapping)
- 位移贴图会真实改变模型,会展现出凸起部分的投影。
- 模型需要足够细致,采样需要足够高。
DirectX使用曲面细分来提高计算效率。
三维纹理
- 利用三维空间中的噪声函数进行纹理映射(例如Perlin Noise)
- 预先进行环境光遮蔽计算模型阴影
- 体渲染通过三维纹理记录信息,然后进行渲染
参考资料
完整笔记
- 度盘链接
- 提取码:njcf











 加油
加油


