关键词:扫描转换、区域填充、裁剪算法
直线扫描转换算法
DDA算法
算法思想:
- x每次+1因此,yi+1=yi+k
- k=y1-y0/x1-x0
- 为了四舍五入,每次y值+0.5后再取整
问题:
- 如果Δx太小则光栅点太稀疏
中点画线法
算法思想:
- 使用一般式方程y=Ax+By+C,若在直线上则F(x,y)=0,在直线上方则>0,下方则<0,其中A=y0-y1,B=x1-x0
- 若k在0和1之间,则x每次+1,y只需要判断+1或者不变若M在Q上方
- 将M点带入一般是方程得出d值,若d<0则取pu,d>0取pd,=0可以任意选取
- 为了求出d值,需要两个乘法,四个加法

算法优化:
- 使用增量思想求出下一个d减少计算量
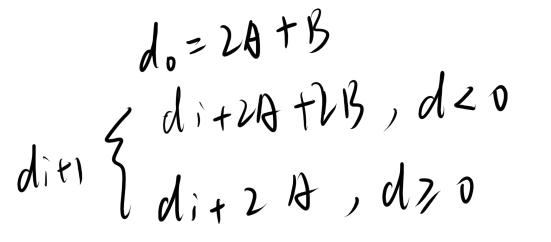
- 若d<0则取y+1,d>=0则不变(这里认为在直线上时y不变)
- 同时为了避免浮点数,d的数值都*2
圆的中点画圆法
算法思想:
- 构造函数F(x)=x²+y²-R²,将M(xp+1,yp-0.5)代入函数构造判别式d
- 首个代入的点为(0,R)因此d=1.25-R
- 根据下个点的像素,得出下个点的判别式
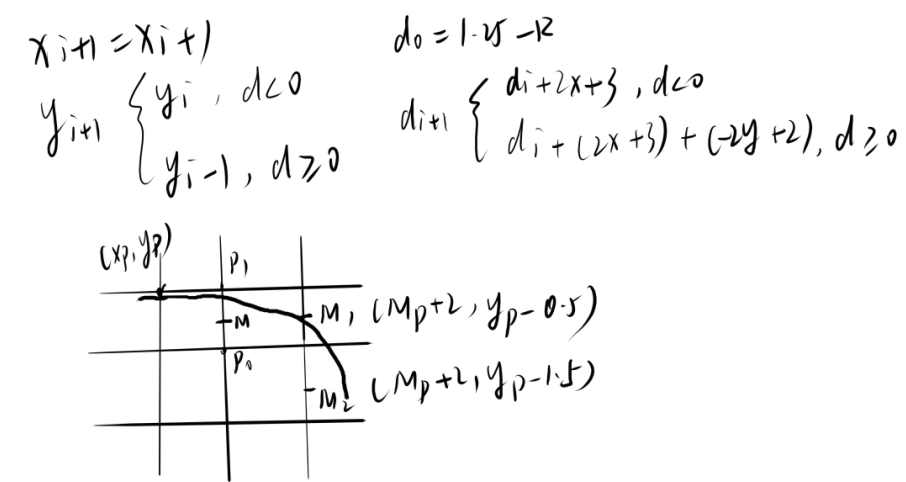
- 只需要画(x<y)第一象限八分之一个圆,其他可以通过(-x,-y),(y,x),(-y,-x)来画
算法优化:
- 让d的初值等于1-r不影响后面计算且少用一个浮点数
- 每当x+1,d+2,每当y-1,d+4

- 因此当d>0(x+=1,y-=1)时,d+=4
区域填充算法
区域:指已经表示为点阵形式的填充图形,是像素的集合
区域填充:将区域中的一点(种子点)赋予给定颜色然后将这个颜色扩散到整个区域的过程
区域可以采用内点表示和边界表示两种表示形式
区域填充算法要求区域是连通的。
有序边表法
对于每一条扫描线的处理 :
- 求交点:首先求出扫描线与多边形各边的交点;
- 交点排序:将这些交点按X坐标递增顺序排序;
- 交点匹配:即从左到右确定落在多边形内部的那些线段;
- 区间填充:填充落在多边形内部的线段。
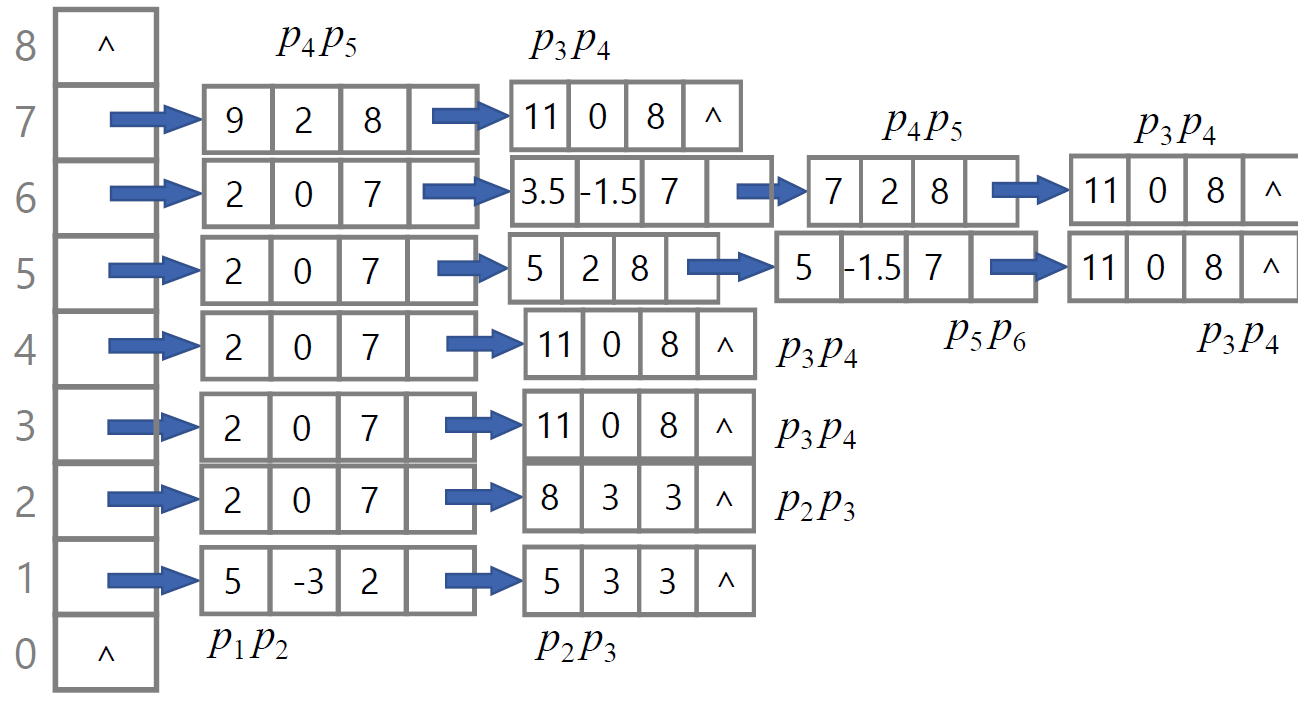
根据下图构建新边表和活性边表
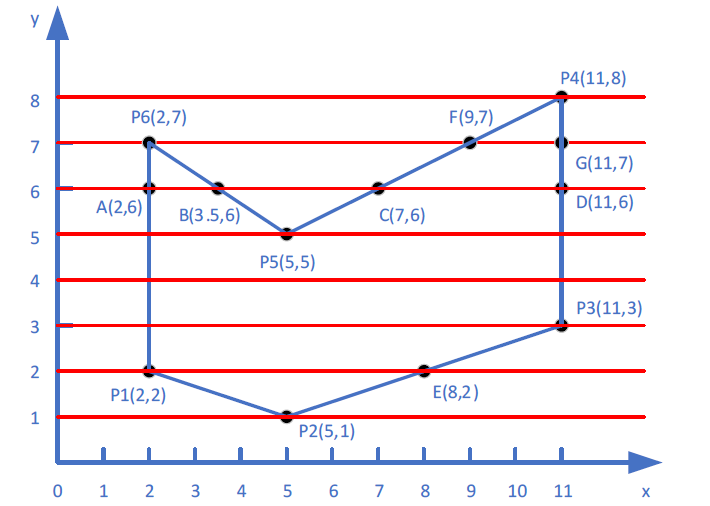
新边表:
- 从0到y依次对每条扫描线进行处理,不需要重复处理
- Ymax:边的最大Y值;
- ΔX:从当前扫描线到下一条扫描线之间的X增量(dX/ dY);
- next:指针,指向下一条边。
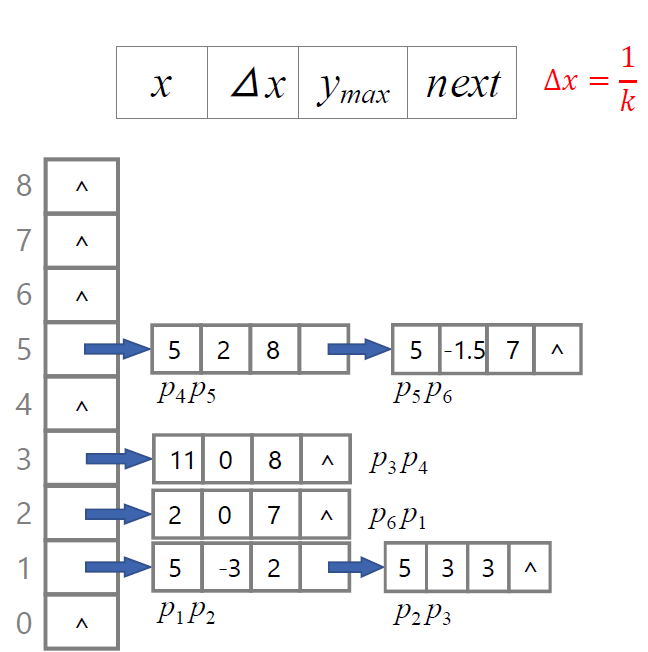
活性边表:
- 每增加一行,x+=Δx,直到y=ymax
- 每行需要根据x排序
栈结构实现种子填充算法
算法思想:
- 种子像素入栈,重复执行下列操作直到栈空
- 栈顶像素出栈
- 将出栈像素置成要填充的颜色
- 按照左上右下的顺序检查与栈像素相邻的四个像素
- 若其中某个像素不在边界且未置成填充色则把该像素入栈
不足之处:
- 有些像素会入栈多次,会降低算法效率且栈结构占用空间
- 递归执行效率不高,费时费内存
裁剪算法
点的裁剪

需要满足以上不等式
直线段的剪裁
直线段的裁剪需要判断:
- 直线段是否完全落在裁剪窗口内
- 是否完全在窗口外
- 计算他与一个或多个裁剪边界的交点
Cohen-Sutherland算法
算法思想:
- 将每个线段分为三个情况处理
- 若线段的两个端点均在窗口外则抛弃线段
- 若线段的两个端点均在窗口内则保留线段
- 若都不满足则将每条线段的端点赋以四位二进制码D3D2D1D0 (上下右左边界)
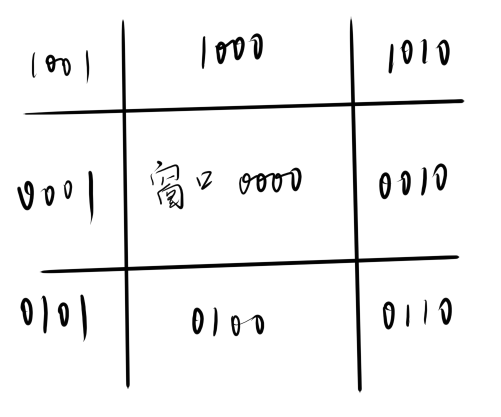
- 求得两个编码后进行逻辑运算
- 若两编码或操作后=0则完全保留
- 若两编码与操作后≠0则直接抛弃
- 求出直线段与窗口边界的交点p3在交点处将线段一分为二,重复上面操作直到满足或操作后=0
中点分割法
算法思想:
- 通过二分逼近来确定直线段与窗口的交点
- 若中点不在窗口内,则中点和离窗口边界最远点形成的线段丢弃,以线段上的另一点再构成线段求其中点
- 若中点再窗口内,则又以中点和最远点构成线段,并求其中点直到终点与窗口边界的坐标值在规定的误差范围内
Liang-Barsky算法
算法思想:
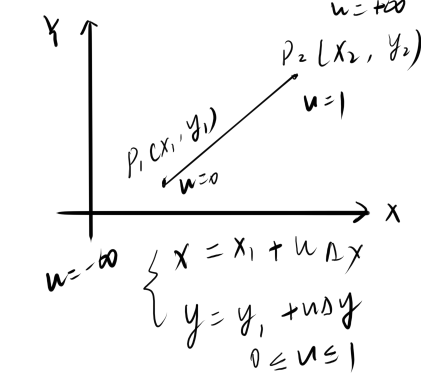
- 用参数方程表示一条直线段
- 把直线段看成一条有方向的线段
- 入边和出边
- 入边有两个交点,出边有两个交代呢,加上直线段两个交点一共有六个端点

- u1=max(0,ul,ub)
- u2=min(1,ut,ur)
多边形裁剪
Sutherland-Hodgeman多边形裁剪
算法思想:
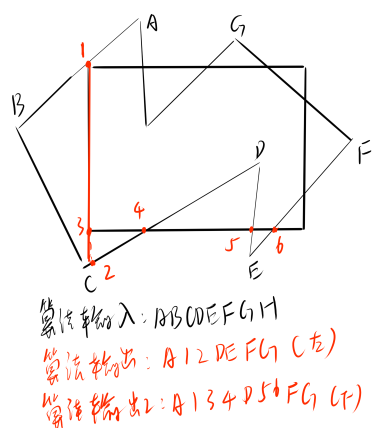
- 将多边形边界作为一个整体,每次用窗口的一条边对要裁剪的多边形和中间结果进行裁剪,体现一种分而治之的思想
- 依次根据下面的输出完成多边形剪裁
文字裁剪
字符裁剪按照精度分为:串精确度裁剪、字符精确度裁剪、笔画/像素精确度裁剪
串精确度:字符串完全在裁剪窗口内则全部保留否则全部舍去
字符精确度:字符串的某个字符方框整个在窗口内时显示字符否则不显示
笔画/像素精确度:具体判断字符串各个像素笔画保留窗口内部分,裁剪窗口外部分
反走样
- 采样频率过低就会造成走样的现象
- 光栅图形产生的阶梯型
- 图形中微小的物体被丢弃或者忽略
- 提高分辨率可以反走样
- 通过在矩形边界附近加入灰色像素来柔化黑到白的尖锐变化’
- 非加权区域采集方法(盒式滤波器)
- 像素的亮度与相交区域的面积成正比,相交面积越大,亮度越高
- 因为每个像素的权值都一样所以仍会造成锯齿
- 加权区域采样方法
- 直线段离像素中心距离越近该像素就会越亮
- 采用离散计算的方式,将像素划分为9个子像素
- 加权方案:中心像素是角像素的四倍,是其他像素的两倍,对九个子像素加权计算出来的亮度进行平均
- 用较高的分辨率计算,然后采用某种平均算法,把结果转到较低分辨率的显示器显示。(线性插值)
- 把每个像素划分为四个子像素,扫描转换算法求得各子像素的颜色值。然后,对每个子像素的颜色值进行简单平均,得到像素的颜色值。











 加油
加油

