概述

推荐阅读：傅里叶分析之掐死教程（完整版）https://zhuanlan.zhihu.com/p/19763358

傅里叶变换的核心

任何周期函数都可以表示为不同频率的正弦和/余弦和的形式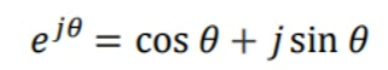（欧拉公式）

什么是欧拉公式

欧拉公式是复分析领域的公式，他将三角函数和负指数函数联系起来，因此负指数函数是周期，因为它可以描述成正弦函数与余弦函数的叠加。

傅里叶变换的公式

为什么傅里叶变换可以用于图像滤波

在时域很难将某些频率成分去掉，但是转换到频率域之后，不同的评率对应的致死频率轴上一个固定的值，将该值设置为0应该是一家很简单的事情，这就是为什么要用傅里叶变化的根本原因。

二维傅里叶变换

概述

公式

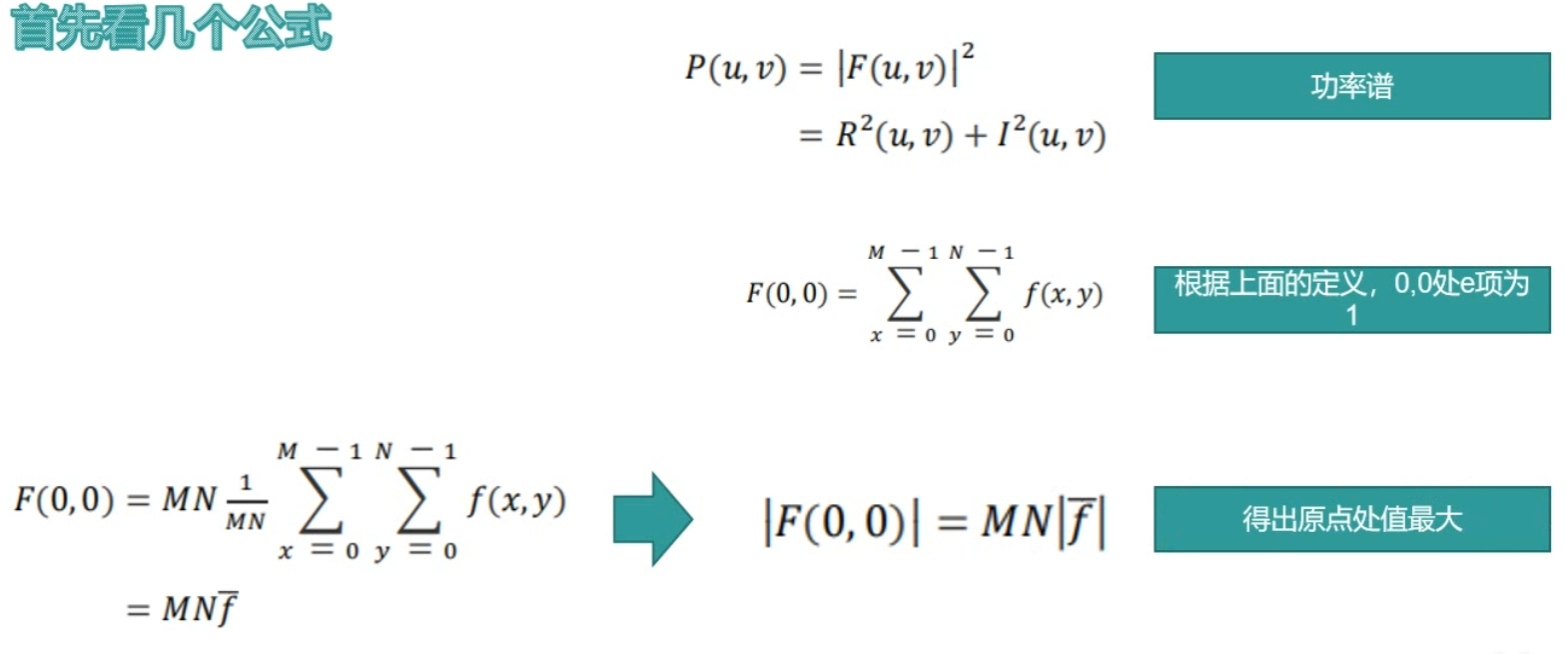
说明：功率谱、频率谱、相位谱的尺寸与图形尺寸一致，都是M*N

频谱图的处理

如何理解 图像傅里叶变换的频谱图：https://blog.csdn.net/m0_51233386/article/details/115134101

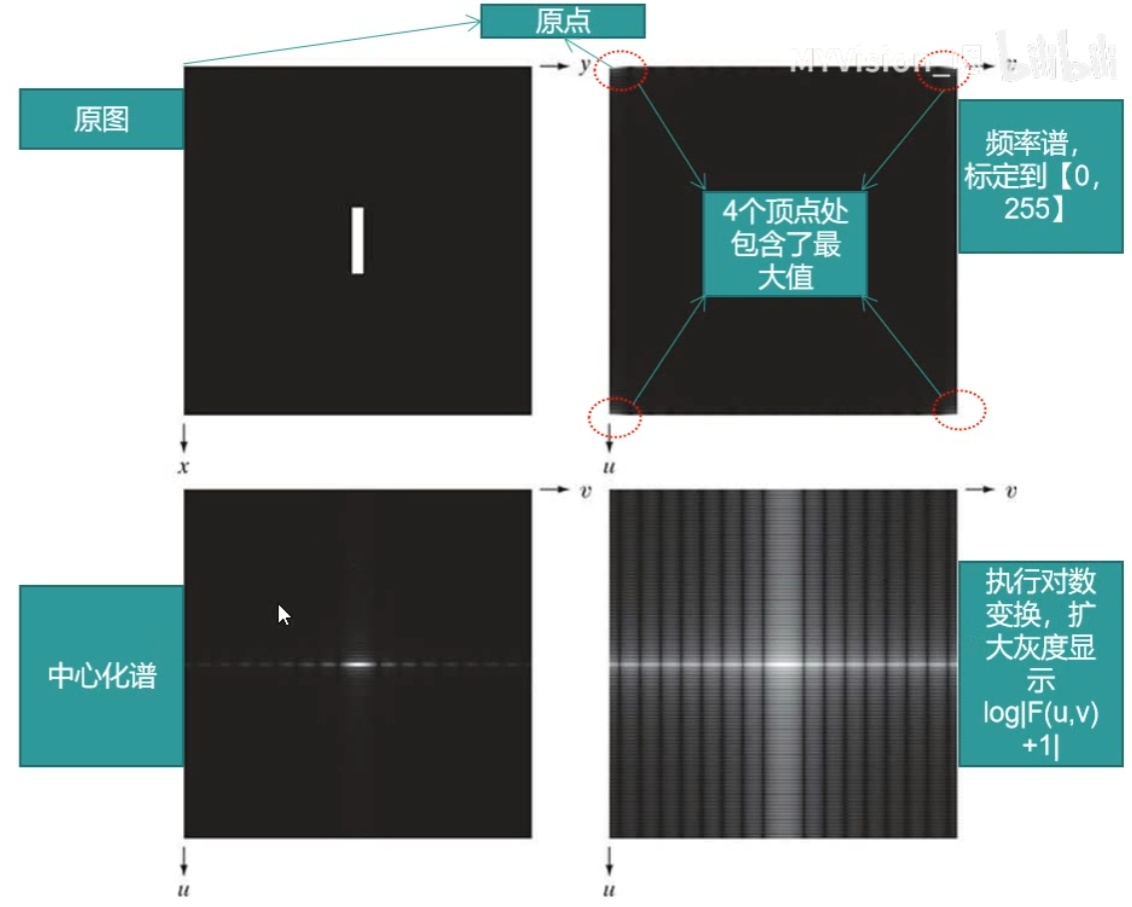
原图做傅里叶变化得到右上角的图，四周为低频，中心为高频，中心化后中间为低频四周为高频

频谱取决于正弦波的幅度，在给定的频率处幅度较大意味着该频率的正弦波比较突出

旋转平移对频谱图的影响

• 平移对频谱图没有任何影响
• 频谱图像跟着原始图像的选择一致

旋转平移对相位谱的影响

• 相位图与图像变换的关系不是很强，但是它绝对了各个正弦分量关于原点位移的度量
• 相位图关于原点对称
• 变换后中心是频率域原点，强度最大，为直流分流
• 相位图中越亮的位置标示该点对应的正弦波的振幅较大

频率域滤波基础

空间域频率与频率域滤波的对应关系

结合两者优点

• 首先我们在频率域选择一个比较好的滤波器，然后我们将该滤波器求傅里叶反变换得到空间域滤波器，再取样生成空间域的滤波模板
• 频率于滤波器越窄，其衰减的高频越多，引起的模糊越大，对应到空间域则需要用加大的模板来增大模糊

频率域滤波原理

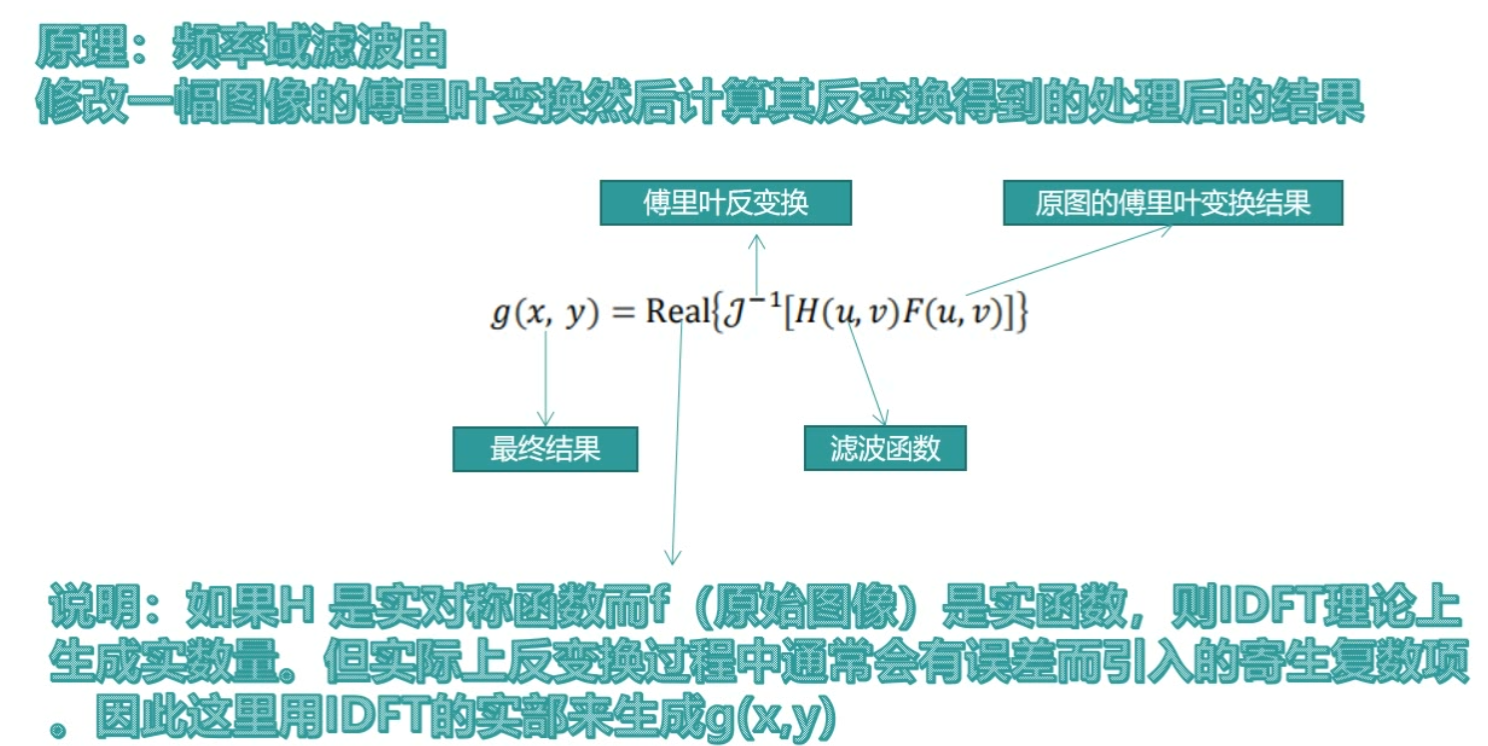
频率域滤波的步骤

频率域平滑滤波器

理想低通滤波器

概述

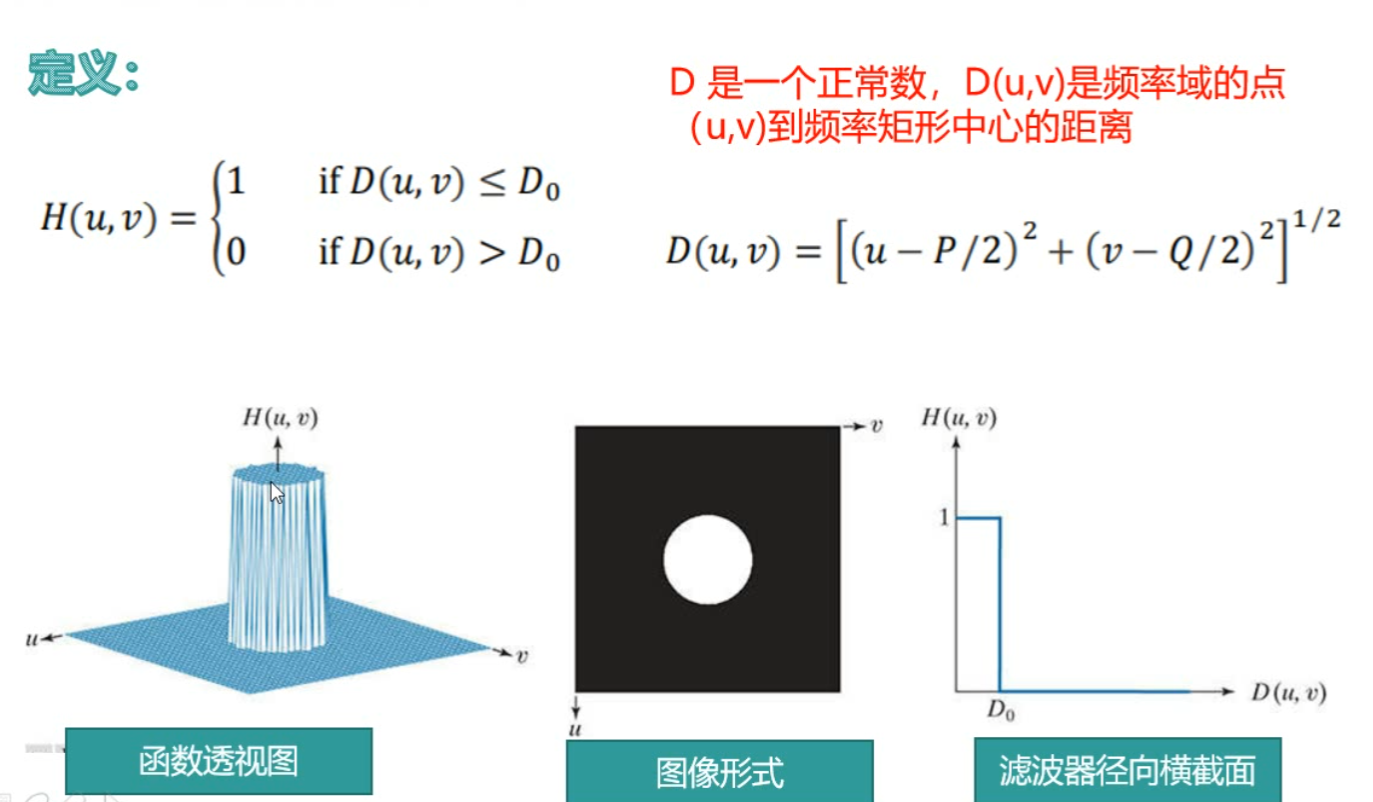
• 在半径为D0的圆内，所有频率无衰减的通过，在圆外完全被衰减，关于原点径向对称，也就是说定义一个径向截面，然后旋转360°可以得到一个理想低通滤波器。
• D0越小，模糊效果越好

振铃效应

• 低通滤波器后边缘处有波纹的效果，过滤掉额频率越多，振铃效应越明显
• 由于理想低通滤波器的频率域剖面图类似于盒装滤波器，因此其空间域滤波器有sin函数形状，空间域的滤波可以用卷积表示

结论

sinc函数的展开度与H(u, v)滤波函数的半径成反比，D0越大，sinc函数就会道近于个和图像卷积是根本不会发生模糊的冲击,低通滤波的目

标是找到没有振铃或振铃效应很小的滤波器。

三种常见低通滤波器的联系与区别

频率域高通滤波器

参考资料

https://www.bilibili.com/video/BV19F411T7fD（本系列文章就是根据链接里的教程进行整理）