串的定义和基本操作

定义：

  • 串，即字符串（String）是由零个或多个字符组成的有限序列。一般记为S = ‘a1a2······an' （n ≥0）
  • 其中，S是串名，单引号括起来的字符序列是串的值；ai可以是字母、数字或其他字符；串中字符的个数n称为串的长度。n = 0时的串称为空串（用∅表示）。
  • 有的地方用双引号（如Java、C），有的地方用单引号（如Python）
  • 例如：S=”HelloWorld!”T=‘iPhone 11 Pro Max?’
  • 子串：串中任意个连续的字符组成的子序列。Eg：’iPhone’，’Pro M’是串T的子串
  • 主串：包含子串的串。Eg：T是子串’iPhone’的主串
  • 字符在主串中的位置：字符在串中的序号。Eg：’1’在T中的位置是8(第一次出现)
  • 子串在主串中的位置：子串的第一个字符在主串中的位置。Eg：’11 Pro’在T中的位置为8
  • 每个空格字符占1B，不是空串
  • 串的位序从1开始而不是从0开始
  • 串是一种特殊的线性表，数据元素之间呈线性关系
  • 串的数据对象限定为字符集（如中文字符、英文字符、数字字符、标点字符等）
  • 串的基本操作，如增删改查等通常以子串为操作对象，因为人类的语言通常要多个字符组成的序列才有现实意义

串的基本操作：

  • 假设有串T=“”，S=”iPhone 11 Pro Max?”，W=“Pro”
  • StrAssign(&T,chars)：赋值操作。把串T赋值为chars。
  • StrCopy(&T,S)：复制操作。由串S复制得到串T。
  • StrEmpty(S)：判空操作。若S为空串，则返回TRUE，否则返回FALSE。
  • StrLength(S)：求串长。返回串S的元素个数。
  • ClearString(&S)：清空操作。将S清为空串。
  • DestroyString(&S)：销毁串。将串S销毁（回收存储空间）。
  • Concat(&T,S1,S2)：串联接。用T返回由S1和S2联接而成的新串
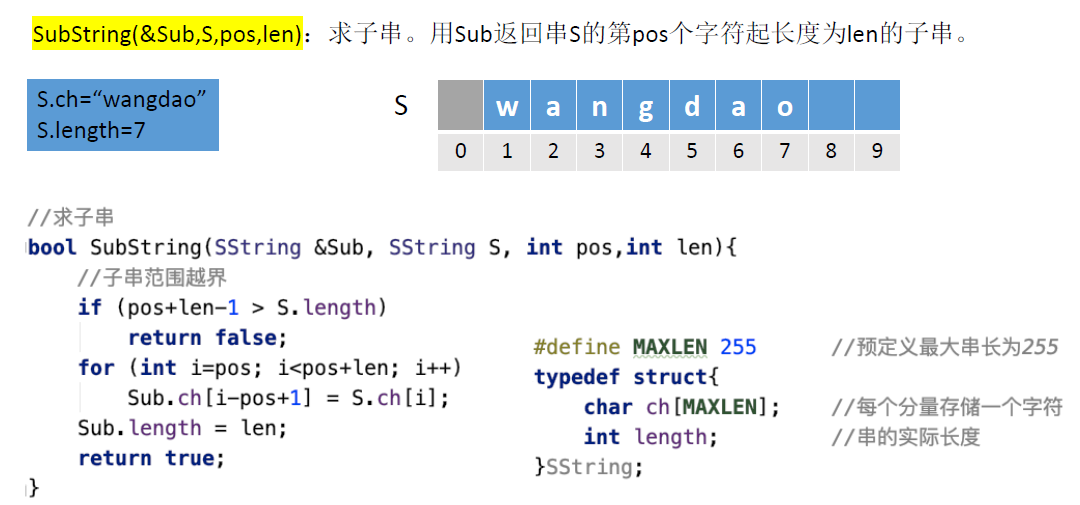
  • SubString(&Sub,S,pos,len)：求子串。用Sub返回串S的第pos个字符起长度为len的子串。
  • Index(S,T)：定位操作。若主串S中存在与串T值相同的子串，则返回它在主串S中第一次出现的位置；否则函数值为0。
  • StrCompare(S,T)：比较操作。若S>T，则返回值>0；若S=T，则返回值=0；若S<T，则返回值<0。
    • 从第一个字符开始往后依次对比，先出现更大字符的串就更大
    • 长串的前缀与短串相同时，长串更大
    • 只有两个串完全相同时，才相等

字符集编码：

  • 任何数据存到计算机中一定是二进制数。
  • 需要确定一个字符和二进制数的对应规则这就是“编码”
  • “字符集”：英文字符，ASCII字符集，中英文，Unicode字符集
  • 基于同一个字符集，可以有多种编码方案，如：UTF-8，UTF-16
  • 注：采用不同的编码方式，每个字符所占空间不同，考研中只需默认每个字符占1B即可

串的储存结构

顺序存储：

image-20220628153926483

  • 方案一：一个数组来储存字符，一个int变量length储存实际长度
  • 方案二：数组的ch[0]来充当length，优点：字符的位序和数组下标相同
  • 方案三：没有Length变量，以字符’\0’表示结尾（对应ASCII码的0），缺点：获取字符串长度需要遍历，时间复杂度高
  • 方案四：数组的ch[0]废弃不用，从看开始储存字符，外加一个int变量length储存实际长度

链式存储：

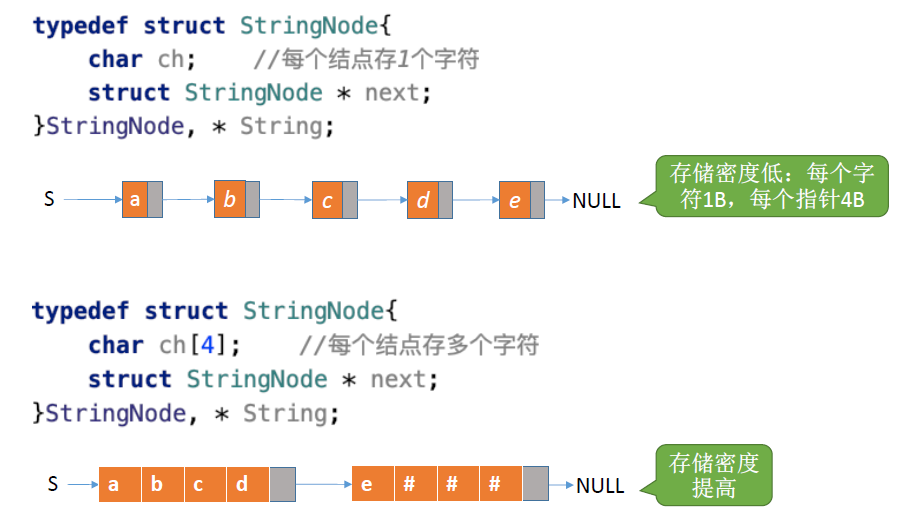
image-20220628154713878

推荐使用第二种方式，存储密度较高，ch数组未必一定是4个字符，也可以比4多

基本操作的实现（使用第四种方案）：

image-20220628163221819

image-20220628172434394

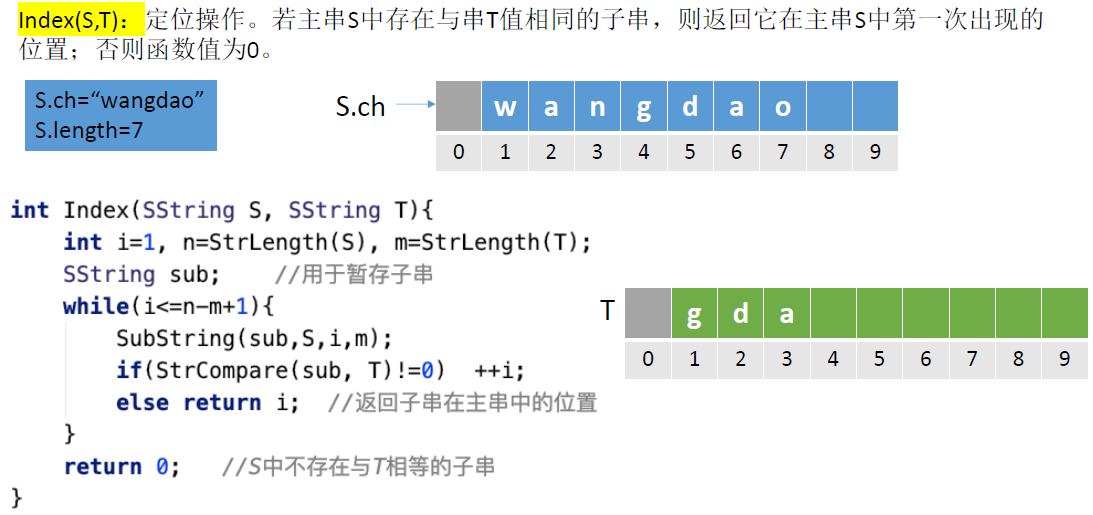
image-20220628173013570

朴素模式匹配算法

字符串模式匹配：

  • 在主串中找到与模式串相同的子串，并返回其所在位置。
  • 子串：主串的一部分，一定存在
  • 模式串：不一定能在主串中找到
  • 要掌握朴素模式匹配算法、KMP算法两种方法

朴素模式匹配算法（两种实现方法）：

  • 将主串中所有长度为m的子串依次与模式串对比，直到找到一个完全匹配的子串，或所有的子串都不匹配为止。
  • 主串长度为n，模式串长度为 m，最多对比 n-m+1 个子串
  • 上节讲的index定位操作就是朴素模式匹配算法中其中一种实现方法
  • 也可以使用两个指针i和j来进行匹配。若当前子串匹配失败，则主串指针 i 指向下一个子串的第一个位置，模式串指针 j 回到模式串的第一个位置，即i = i - j + 2; j = 1;
  • 若 j > T.length，则当前子串匹配成功，返回当前子串第一个字符的位置即i - T.length
  • image-20220628175450990
  • 设主串长度为 n，模式串长度为 m，则最坏时间复杂度 = O(n*m)，最好时间复杂度 = O(n)

KMP算法的概念

  • 由D.E.Knuth，J.H.Morris和V.R.Pratt提出，因此称为 KMP算法
  • 是对朴素模式匹配算法的优化
  • 优化的原理就是减少了i指针的回溯，通过已经计算好的next指针，提高算法的整体运行效率
  • next数组记录了当第几个元素匹配失败时候，j的取值例如：
    • 对于模式串 T = ‘abaabc’
    • 当第6个元素匹配失败时，可令主串指针 i 不变，模式串指针 j=3
    • 当第5个元素匹配失败时，可令主串指针 i 不变，模式串指针 j=2
    • 当第4个元素匹配失败时，可令主串指针 i 不变，模式串指针 j=2
    • 当第3个元素匹配失败时，可令主串指针 i 不变，模式串指针 j=1
    • 当第2个元素匹配失败时，可令主串指针 i 不变，模式串指针 j=1
    • 当第1个元素匹配失败时，匹配下一个相邻子串，令 j=0, i++, j++
  • next数组只和短短的模式串有关，和长长的主串无关（重要）
  • 之所以只和模式串有关，是因为如果在哪里匹配失败，同时说明在这之前的部分主串和模式串是相同的
  • KMP算法，最坏时间复杂度 O(m+n)，其中，求 next 数组时间复杂度 O(m)，模式匹配过程最坏时间复杂度 O(n)
  • KMP算法精髓：利用好已经匹配过的模式串的信息

image-20220628181612375

  • 步骤：
    • 根据模式串T，求出 next 数组
  • 利用next数组进行匹配（主串指针不回溯）

image-20220628202314761

KMP算法之求next数组

next数组的作用：

当模式串的第 j 个字符失配时，从模式串的第 next[j] 的继续往后匹配

next数组的求法：

  • 任何模式串都一样，第1个字符不匹配时，只能匹配下一个子串，因此next[1]都无脑写 0（if(j==0) {i++; j++;}）
  • 任何模式串都一样，第2个字符不匹配时，应尝试匹配模式串的第1个字符，因此next[2]都无脑写 1
  • 每一个模式串不一样，对于第3个字符及之后的字符串，在不匹配的位置前边，划一根美丽的分界线模式串一步一步往后退，直到分界线之前“能对上”，此时 j 指向哪儿，next数组值就是多少

KMP算法之求nextval数组

定义：

nextval数组是对next数组的优化，用nextval替代next数组，减少了无意义的对比

nextval数组的求法：

  • 先根据上面的方法算出next数组
  • 先令nextval[1]=0
  • 再根据下面代码算出后面的nextval数组
  • for(int j = 2; j <= T.length; j++)
{
    //让第next值个元素的值和当前元素比较
    if(T.ch[next[j]] == T.ch[j])
    {
        //若相等则让第next值个元素的nextval值复制给当前元素的nextval值
        nextval[j] = nextval[next[j]];
    }
    else
    {
        //若不等则让当前元素的next值赋值给当前元素的nextval值
        nextval[j] = next[j];
    }
}

笔记完整PDF

百度网盘提取码：l3ja

赏